Abstract
This post presents the results of using the Least-Squares Support Vector Machines (LS-SVMs) framework for estimating CO\(_{2}\) levels at the Holst Center building in the Netherlands. Within the IoT framework, a Wireless Sensor Network (WSN) consisting of seven sensors is currently deployed at different locations on the third floor of the building. A network consisting of seven sensors nodes is currently deployed at different locations in the third floor of the building. Each sensor node provides measures of temperature, relative humidity and CO\(_{2}\) levels, and wirelessly transmits the readings to a consumer accessible cloud. Given that CO\(_{2}\) has a big impact on people comfort and productivity, its monitoring and control has become a common practice in recent years. In this work we provide a way to estimate the CO\(_{2}\) concentration when a CO\(_{2}\) sensor is not trustworthy (e.g., due to maintenance or a malfunction), by using nonlinear models built from historical sensor data. Results showed that the model structures proposed in this work provided better CO\(_{2}\) estimates than those given by conventional linear autoregressive (AR) and autoregressive exogenous (ARX) models.
This post is inspired my the work published in Data-driven modeling techniques for indoor CO2 estimation [1]. The full list of authors of this paper are;
- Bob Vergauwen
- Oscar Mauricio Agudelo
- Raj Thilak Rajan
- Frank Pasveer
- Bart De Moor
Introduction
Indoor air quality is one of the main contributors to the well-being and comfort inside a building. Typically the term air quality is associated with several parameters including, temperature, humidity, concentration of Volatile Organic Compounds (VOC) and CO\(_2\). In recent studies it has been shown that in high concentration, CO\(_{2}\) has a negative effect on the cognitive function of the people inside a building [2].
For this reason, monitoring and controlling the levels of CO\(_{2}\) in a building is of great importance in creating an optimal environment inside the building.
In order to design an optimal control strategy for the heating, ventilation and air conditioning (HVAC) a good model of the building climate parameters in needed. The focus on such a model should not lie on the physical representation of the buildings thermodynamical properties but on the prediction capabilities of the model. Predicting the evolution of the CO\(_{2}\) concentration is the biggest challenge in this modeling problem. A second application of CO\(_{2}\) models is to combine measurements with model predictions to improve the accuracy of the CO\(_{2}\) sensors or even to replace short sequences of missing data and thereby make the measurement system more robust.
Some attempts have been made to model CO\(_{2}\) in order to design an optimal control strategy. For example in [3] an estimation of the human activity is used to predict the values of CO\(_{2}\) over time.
Currently in the third floor of the Holst Center building in Eindhoven (The Netherlands), several sensors nodes measuring temperature, relative humidity and CO\(_{2}\) monitor the ambient conditions and make sure that the personnel is not subjected to adverse conditions that can affect their well-being and productivity. However it is not uncommon to find a CO\(_{2}\) sensor that is down due to technical problems.
In this work we propose to use the Least-Squares Support Vector Machines (LS-SVMs) framework to construct nonlinear models that can be used to estimate the CO\(_{2}\) levels when a sensor is down. These models exploit the correlations between CO\(_{2}\) and other variables such as temperature, relative humidity and calendar information of occupancy. Spatial correlations between nearby nodes are also exploited to improve the quality of the CO\(_{2}\) estimates.
This article is organized as follows. Section presents a brief description of the sensor network in the Holst Center building as well as the characteristics of the sensor nodes. In Section, the non-linear modelling approach used in this work is described. Section shows the results of evaluating different model structures under different CO\(_{2}\) estimation scenarios. In Section some concluding remarks are given.
Sensor Network
IMEC-Holst center is currently rolling out a Wireless Sensor Network (WSN) within the IoT framework, capable of measuring air-quality of the environment and communicating this information to a consumer accessible cloud. Each node in the network is a heterogeneous platform containing a variety of sensors for air pollutants (such as CO\(_2\), NO2, PM) and environment monitoring (such as temperature, humidity, sound). The sensor nodes are in-house designed boards at IMEC-NL, which also incorporates the TI SimpleLink Sensor tag CC2650. The board router is a Raspbery Pi, whose primary job is to collect data from the sensor nodes in the network. The Figure 1 does not depict this node, since the board router is not equipped with sensors. The IMEC-Holst center platform is designed to be customizable, wherein the number of nodes can be extended and in a given node, desired air quality sensors can be chosen prior to deployment. Such a network offers spatio-temporal information on the air-quality of the environment, which must be processed efficiently for desired feature extraction. In such networks, one of the key challenges is to estimate CO\(_{2}\) levels when the sensor data is untrustworthy.
Figure 1 shows the spatial distribution of an indoor deployment of a sensor network of \(7\) nodes in the Holst center. The nodes are arbitrarily deployed in office spaces, corridors and labs. Each node contains various sensors including COZIR CO\(_{2}\) sensor [4], SHT21 - temperature and relative humidity sensor [5]. Each node samples a sensor modality approximately once every \(30\) seconds. The COZIR CO\(_{2}\) offers an accuracy of \(\pm 50\) ppm with a range of \(0-2000\) ppm, while the temperature and humidity sensors are accurate up to \(\pm\) 0.3 celsius and \(\pm 2 \%\) respectively. The data from the nodes is collected by a board-router and then transmitted via WiFi to the cloud for storage and processing. The board router is a Raspbery Pi, whose primary job is to collect data from the sensor nodes in the network. Figure 1 does not depict this node, since the board router is not equipped with sensors. The protocol stack employed to realize the sensor network includes IEEE 802.15.4 in the physical layer and Contiki MAC in the data link layer.
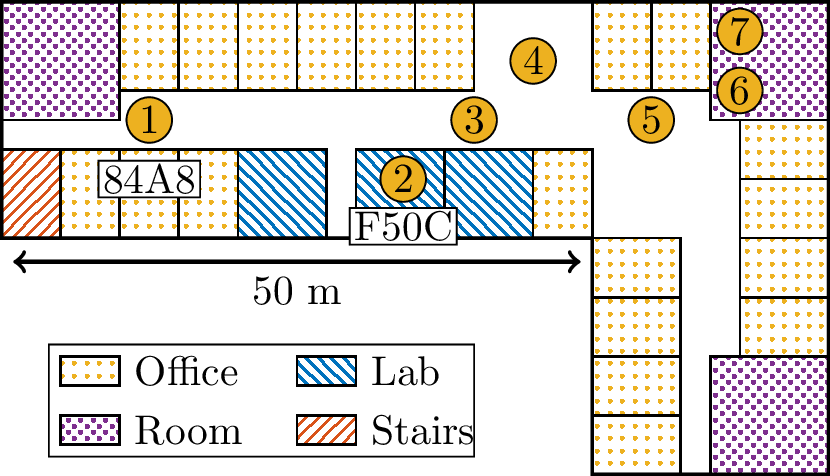
Figure 1: Sketch of the third floor plan of the Holst Center building with the location of the sensor nodes.
Nonlinear Modelling
In order to model the evolution of the CO\(_2\) concentration, we first tried linear models, namely, autoregressive (AR) and autoregressive exogenous (ARX) models. However the best results were obtained with the nonlinear autoregresive exogeneous (NARX) model structure defined as follows:
\begin{align} \label{eqn:model} y_t = f(y_{t-1}, &y_{t-2}, \ldots, y_{t-n_y}, \\ &\mathbf{u}_t,\mathbf{u}_{t-1},\ldots, \mathbf{u}_{t-n_u}) + e_t, \nonumber \end{align}
where \(y_t \in \real\) is the output variable at time \(t\), i.e., the CO\(_2\) concentration, \(u_t \in \real^d\) is the vector of the exogenous input variables (e.g., temperature, relative humidity, calendar information, etc.), \(n_y\) and \(n_u\) are the number of lags for \(y_t\) and \(u_t\) respectively, and \(e_t\) is assumed to be a white noise process. Nonlinear effects can be identified when \(f(\cdot)\) is parameterized as a nonlinear function. Here we use the Least-Squares Support Vector Machines (LS-SVMs) [6] framework to estimate this nonlinear function from historical data.
Function estimation using LS-SVM
LS-SVMs are a class of kernel methods that use positive-definite kernel functions to construct a non-linear representation of the original inputs in a high-dimensional feature space [6]. Notice that we can rewrite the NARX model given in Equation \(\eqref{eqn:model}\) in the following way:
\begin{equation} \label{eqn:equ2} y_t = \mathbf{w}^{T} \boldsymbol{\varphi}(\mathbf{x}_t) + b + e_t, \end{equation}
where \(y_t \in \real\), \(\mathbf{x}_t \in \real^n\) is the regression vector \(\left[ y_{t-1}, y_{t-2}, \ldots, y_{t-n_y}, \mathbf{u}_t,\mathbf{u}_{t-1},\ldots, \mathbf{u}_{t-n_u} \right]\), \(\mathbf{w} \in \real^{n_h}\) is an unknown weighting vector, \(b\) is the bias term and \(\boldsymbol{\varphi}(\cdot):\mathbb{R}^{n}\rightarrow\mathbb{R}^{n_h}\) is a nonlinear feature map that converts the original input \(\mathbf{x}_t \in \real^n\) to a high-dimensional (possibly infinite-dimensional) vector \(\boldsymbol{\varphi}(\mathbf{x}_t) \in \real^{n_h}\). This is an example of a black box model, this means that the internal parameters of the model can not be related to physical properties of the real system. In order to estimate the unknown \(\mathbf{w}\) and \(b\), we formulate the following optimization problem,
\begin{align} \label{eqn:lsp} &\underset{\mathbf{w},b,\mathbf{e}}{\min} \hspace{2mm}\dfrac{1}{2}\mathbf{w}^{T} \mathbf{w} + \dfrac{\gamma}{2} \sum_{t=1}^{N}e_{t}^{2} \\ \text{s.t.} \hspace{2mm} y_{t} = &\mathbf{w}^{T} \boldsymbol{\varphi}(\mathbf{x}_{t}) + b + e_{t}, \ \ t=1, \ldots,N, \nonumber \end{align}
with \(\gamma > 0\) the regularization parameter and \(N\) the number of data points. This optimization problem can be solved by using the Lagrange multipliers method [7]. First the Lagrangian function \(\boldsymbol{\mathcal{L}}(\cdot)\) is constructed,
\begin{multline} \boldsymbol{\mathcal{L}}(\mathbf{w},b,e,\alpha) = \dfrac{1}{2}\mathbf{w}^{T}\mathbf{w} + \dfrac{1}{2}\gamma \sum_{t=1}^{N}e_{t}^{2}\\ -\sum_{i=1}^{N}\alpha_{t}(\mathbf{w}^{T} \boldsymbol{\varphi}(\mathbf{x}_{t}) + b + e_{t}-y_{t}), \end{multline}
with \(\alpha_t \in \real\) the Lagrange multipliers, and then the optimality conditions are evaluated (\(\frac{\partial \boldsymbol{\mathcal{L}}}{\partial \mathbf{w} }=0\), \(\frac{\partial \boldsymbol{\mathcal{L}}}{\partial b }=0\), \(\frac{\partial \boldsymbol{\mathcal{L}}}{\partial e_t}=0\), \(\frac{\partial \boldsymbol{\mathcal{L}}}{\partial \alpha_t }=0\) ) in order to generate a system of linear equations, from which the values of \(\alpha_t\) and \(b\) can be obtained. The final expression for the estimated \(f(\cdot)\) is given by
\begin{equation} \label{eqn:equ_dual} \hat f (\mathbf{x}) = \sum_{t=1}^{N}\alpha_{t}K(\mathbf{x},\mathbf{x}_{t}) +b, \end{equation}
where \(K(\mathbf{x}_{i},\mathbf{x}_{j})=\boldsymbol{\varphi}(\mathbf{x}_{i})\boldsymbol{\varphi}(\mathbf{x}_{j})^{T}\) is a positive definite Kernel function. Notice that \(\boldsymbol{\varphi}(\cdot)\) does not have to be explicitly computed as this is done implicitly through the positive definite kernel function. In this work the Gaussian Radial Basis Function (RBF) kernel has been used given its properties as universal function approximator when used with LS-SVMs. This kernel takes the form:
\begin{equation} \label{eqn:kf} K(\mathbf{x}_{i},\mathbf{x}_{j}) = \exp \left( \frac{-\left\| \mathbf{x}_{i} - \mathbf{x}_{j} \right\|_2^2}{\sigma^2} \right), \end{equation}
where \(\sigma\) is the kernel parameter.
Fixed-sized LS-SVM
For large-scale problems when the number of data points \(N\) is very large (like the problem treated in this study), solving the linear system equations to compute \(\alpha_t\) and \(b\) becomes challenging due to memory constraints and computational requirements. Although the LS-SVM optimization problem Equation \(\eqref{eqn:lsp}\) is mostly solved in its dual form as shown in the previous section (after applying the Lagrange multipliers method), the problem can also be solved in the primal space, where the size of the vector of unknowns is proportional to the feature vector dimension and not to the number of datapoints. Fixed-sized LS-SVM solves Equation \(\eqref{eqn:lsp}\) in the primal space by estimating a finite-dimensional sparse approximation of the nonlinear feature mapping \(\boldsymbol{\varphi}(\cdot)\) from a subsample of selected data points (support vectors) from the entire dataset [6].
Experiments
This section presents results obtained when NARX models with different exogenous inputs were used to estimate CO\(_{2}\) levels at sensor locations indicated in Figure 1. The dataset used in this work consists of recordings of temperature in [K], relative humidity in [\(\%\)], and CO\(_{2}\) levels in [ppm] during a three-month period. Before using the dataset for training and testing the models, it was necessary to preprocess the data to properly deal with duplicated records, invalid data values, missing data, irregular sampling time and lack of synchronization between the time series generated by the sensor nodes. In order to generate data with a uniform sampling time, the original data was linearly interpolated and resampled with a constant sampling time of 5 minutes.
Based on the quality of the data, we initially focused on modelling the CO\(_{2}\) levels registered by sensor node 84A8, which is located in the corridor next to the staircase exit. During the experiment time period, the ventilation system was ON on workdays from \(0600\) hrs until \(2100\) hrs.
For training the models we used 6469 data points covering the period between March 20th, 2016 and April 21st, 2016. The models were tested in the period between April 22nd, 2016 and April 28th, 2016. The test data set in this case consists of 1941 data points. Given the size of the training data set, we used fixed-sized LS-SVM with 100 support vectors to estimate the nonlinear function \(f(\cdot)\) in all the cases. In this study, we evaluated the following NARX structures:
- NARX-TH: This model structure has the temperature and relative humidity at the node location as exogenous inputs.
- NARX-THC: In addition to temperature and humidity inputs, this model structure incorporates occupancy information of the building using calendar information. We do this by adding two additional exogenous boolean inputs [1, 0] and [0, 1] to indicate weekdays and weekends..
- NARX-THCO: Furthermore, we extend the NARX-THC model using the CO\(_{2}\) readings of the sensor node F50C, which is the closest sensor node to 84A8.
In all these NARX structures we got the best results when \(n_y = n_u = 8\). The kernel parameter of each model was found by carrying out a grid-search. Conventional autoregressive (AR) and autoregressive exogenous (ARX) models were also considered in this study. In particular, we used the so-called naive forecast model (\(y_t=y_{t-1}\)), which is the simplest model that we can construct, and an ARX model with temperature and relative humidity as exogenous inputs. This model is referred to as ARX-TH.
Using the test data set, the models were evaluated in different scenarios, i.e., when the CO\(_{2}\) sensor is down for 5 (1 sampling period), 10 (2 sampling periods), 20 (4 sampling periods), 60 (12 sampling periods) and 120 minutes (24 sampling periods). Note that when the CO\(_{2}\) sensor is unreliable for more than one sampling period, the models are used in a recursive fashion. In order to quantify the quality of the model estimates, we computed the Root Mean Square Error (RMSE) between estimates and CO\(_{2}\) measurements. RMSE values for the different models are presented in Figure 2. It is clear that NARX-TH provides much better estimates than the naive model and the ARX-TH model, especially when the sensor is down for longer periods of time. Adding calendar information leads to a marginal improvement in the CO\(_{2}\) estimates, as can be observed from the results obtained with the NARX-THC model. Finally from the performance of the NARX-THCO model, it is clear that using CO\(_{2}\) readings from a nearby sensor can provide an extra improvement of the CO\(_{2}\) estimates. Similar results were obtained for other sensor nodes, which are not presented due to space limitations.
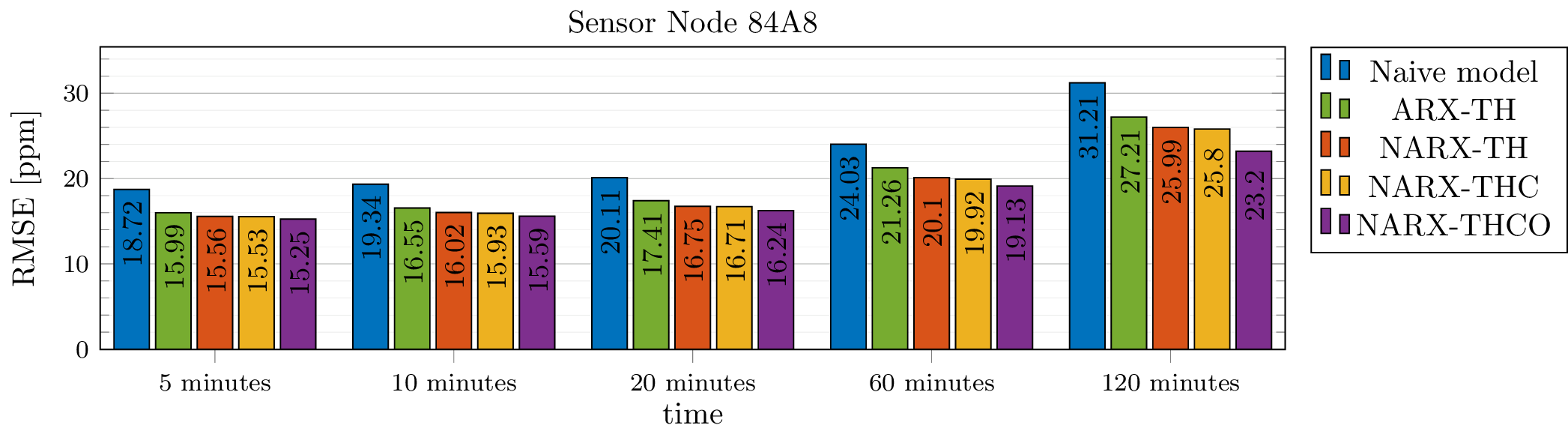
Figure 2: RMSE of the CO({2}) estimates made by the naive forecast model, the ARX-TH model and the NARX models when the CO({2}) sensor of node 84A8 is down for 5, 10, 20, 60 and 120 minutes.
Concluding Remarks
We presented the results of using nonlinear modelling techniques such as fixed-size LS-SVMs for indoor CO\(_{2}\) estimation. Three NARX structures were proposed, namely, NARX-TH, NARX-THC, and NARX-THCO. These model structures were evaluated using data from sensor node 84A8 under different estimation scenarios. The NARX-THCO model provided the best CO\(_{2}\) estimates, especially for the cases when the CO\(_{2}\) sensor is down for longer periods of time. This model exploits the correlations between temperature, relative humidity and CO\(_{2}\), as well as the correlations between the CO\(_{2}\) readings of nearby sensors. In the near future, the sensor network will be extended to more or less 50 sensor nodes. In this case a Nonlinear Multiple-Input Multiple-Output model will be considered to properly capture the correlations between the sensors nodes.