At the core of the presented identification algorithms is the concept of a Hankel matrix. Hankelization of time series is a way of restructuring observed time series data in order to be able to estimate the linear relation between subsequent data points. The resulting matrix is called a Hankel matrix.
In this chapter we will first introduce the Hankel matrix for one-dimensional time series data, followed by two extensions covering multi-dimensional time series. Both extended definitions of the Hankel matrices is connected to the previously introduced observability and recursive observability matrices.
The Hankel matrix
Definition
The classical Hankel matrix defined for a time series \(y = [y_0, y_1, \cdots, y_N]\), containing \(N+1\) data points, is given by
\begin{equation}\label{eqn:Hankel_no_data} Y_{0|p-1} = \begin{bmatrix} y_0 & y_1 & y_2 & \cdots & y_{N-p+1} \\ y_1 & y_2 & y_3 & \cdots & y_{N-p+2} \\ y_2 & y_3 & y_4 & \cdots & y_{N-p+3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ y_{p-1} & y_{p} & y_{p+1} & \cdots & y_{N} \\ \end{bmatrix}. \end{equation}
The subscript in the notation \(Y_{0|p-1}\) denotes the data index of the first column and was already used in the previous chapters. The first element of this column is \(y_0\) and the last one \(y_{p-1}\). This notation is extensively used by Van Overschee in his work on subspace methods~\cite{van2012subspace}. The subscript clearly indicates the data contained in the first column of the Hankel matrix.
In the case where the time series data is generated by a system with multiple outputs, say \(q\) outputs, every element \(y_i\) is a vector with \(q\) elements, in which case the Hankel matrix has \(qp\) rows.
A sliding window
The construction of the Hankel matrix can be visually related to a sliding window that slides over time series data. To construct a Hankel matrix with \(p\) rows, we define a window of size \(p\) and place it over the time series data. The first column of the Hankel matrix is than equal to the elements of the time series that are covered by the window. To generate the next column of the Hankel matrix, we move the window with one step ahead. The index of the data that is covered by the window runs from \(1\) to \(p+1\). These \(p\) points are the elements that form the second column of the Hankel matrix. The process continues until the window reaches the end of the time series data. This method to create a Hankel matrix is graphically represented in Figure~\ref{fig:Hankel_window_1d}.
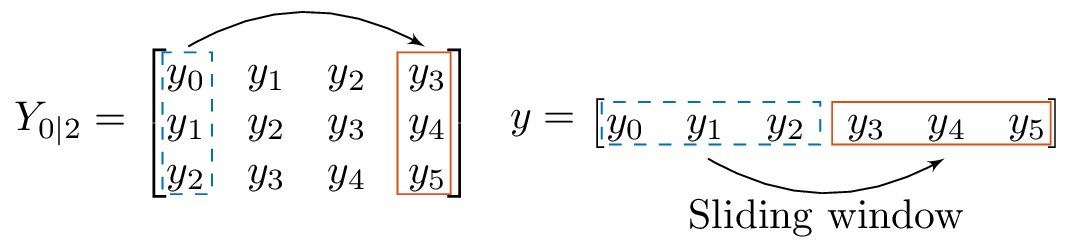
Figure 1: The construction of a Hankel matrix can be interpreted by a window sliding over the time series data. The length of the window determines the number of rows of the Hankel matrix. The first column of the Hankel matrix (indicated with the dashed-box) contains the windowed data at index zero. The last column of the Hankel matrix (indicated with the solid-box) contains the data when the end of the window reaches the last data point. The window slides over the data following the direction of the arrow, from left to right.
Factorization of the Hankel matrix
A Hankel matrix can be factorized as the outer product of the observability and state sequence matrix when the elements of the matrix are the output of a regular or singular state space model. Both cases are discussed in this section.
Regular systems
Consider the one-dimensional state space model \((C,A)\) of order \(m\) with \(q\) outputs and initial state \(x\). The output is given by \(y = [y_0,y_1,\cdots,y_N]\). We assume the system to be observable and controllable. The output of this model at positive index \(k\leq N\) is equal to \(y[k] = CA^kx\). By substituting the expression for the output of the state space model as the elements of the Hankel matrix of Equation~\eqref{eqn:Hankel_no_data} we get
\begin{equation} Y_{0|p-1} = \begin{bmatrix} Cx & CAx & CA^2x & \cdots & CA^{N-p+1}x \\ CAx & CA^2x & CA^3x & \cdots & CA^{N-p+2}x \\ CA^2x & CA^3x & CA^4x & \cdots & CA^{N-p+3}x \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ CA^{p-1}x & CA^{p}x & CA^{p+1}x & \cdots & CA^{N}x \\ \end{bmatrix}. \end{equation}
This matrix can be factorized as
\begin{equation} Y_{0|p-1} = \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{p-1} \end{bmatrix} \begin{bmatrix} x & Ax & A^2x & \cdots & A^{N-p+1}x \end{bmatrix}, \end{equation}
which is the outer product of an extended observability matrix and extended state sequence matrix for regular systems.
Singular systems
A similar factorization result can be obtained for singular systems. Given the time series \(y = [y_0,y_1,\cdots,y_N]\), which is the output of the commuting matrix pencil \((A,E)\) of size \(m\times m\), with output matrix \(C\in \real^{q\times m}\) and generalized state \(x\). The output of the system at index \(k\) is equal to
\begin{equation} y_k = C \mathcal{A}^k_N x = C A^k E^{N-k}x. \end{equation}
The Hankel matrix with \(p\) rows is than
\begin{equation} Y_{0|p-1} = \begin{bmatrix} C\mathcal{A}^0_Nx & C\mathcal{A}^1_Nx & \cdots & C\mathcal{A}^{N-p+1}_Nx \\ C\mathcal{A}^1_Nx & C\mathcal{A}^2_Nx & \cdots & C\mathcal{A}^{N-p+2}_Nx \\ \vdots & \vdots & \ddots & \vdots \\ C\mathcal{A}^{p-1}_Nx & C\mathcal{A}^{p}_Nx & \cdots & C\mathcal{A}^N_Nx \end{bmatrix}. \end{equation}
This matrix can be factorized as
\begin{equation}\label{eqn:1S-Hankel-factor-1} Y_{0|p-1} = \begin{bmatrix} C\mathcal{A}_{p-1}^0 \\ C\mathcal{A}_{p-1}^1 \\ \vdots \\ C\mathcal{A}_{p-1}^{p-1} \\ \end{bmatrix} \begin{bmatrix} \mathcal{A}_{N-p+1}^0 x & \mathcal{A}_{N-p+1}^1 x & \cdots & \mathcal{A}_{N-p+1}^{N-p+1} x & \end{bmatrix}, \end{equation}
which is the outer product of an extended observability matrix and extended state sequence matrix for singular systems.
Generalizations of the Hankel matrix
In this section we present two generalizations of the classical one-dimensional Hankel matrix; the Vandermonde matrix and the recursive Hankel matrix. These two generalizations are linked to the previously introduced generalizations of the observability and state sequence matrices. We will demonstrate that the Vandermonde matrix is the outer product of the observability matrix and the state sequence matrix, whereas the recursive Hankel matrix factorizes as the outer product of the recursive observability and recursive state sequence matrices.
Vandermonde matrix
% An important characteristic that is used in classical one-dimensional realization theory is the fact that the Hankel matrix can be factorized as the product between an observability matrix and a state sequence matrix. Both the observability matrix and the state sequence matrix for commuting state space models have been introduced in Chapters~\ref{ch:2DR} and~\ref{ch:2DS}. For the two-dimensional commuting state space model with system matrices \(A, B\), output matrix \(C\), and initial state \(x\), the first 6 rows of the observability matrix are equal to
\begin{equation*} \obs = \left[ \begin{array}{c|cc|ccc} C^T & (CA)^T & (CB)^T & (CA^{2})^T & (CAB)^T & (CB^{2})^T \end{array} \right]^T. \end{equation*}
Similarly, the first 6 columns of the state sequence matrix are
\begin{equation*} X = \left[ \begin{array}{c|cc|ccc} x & Ax & Bx & A^{2}x & ABx & B^{2}x \end{array} \right]. \end{equation*}
The outer product of both matrices is
\begin{equation} \left[ \begin{array}{c|cc|ccc} Cx & CAx & CBx & CA^2x & CABx & CB^2x \\ \hline CAx & CA^2x & CABx & CA^3x & CA^2Bx & CAB^2x \\ CBx & CABx & CB^2x & CA^2Bx & CAB^2x & CB^3x \\ \hline CA^2x & CA^3x & CA^2Bx & CA^4x & CA^3Bx & CA^2B^2x \\ CABx & CA^2Bx & CAB^2x & CA^3Bx & CA^2B^2x & CAB^3x \\ CB^2x & CAB^2x & CB^3x & CA^2B^2x & CAB^3x & CB^4x \end{array} \right]. \end{equation}
By substituting the expression for the output of a commuting state space model \(y_{k,l} = CA_1^kA_2^lx\), we get
\begin{equation} \left[ \begin{array}{c|cc|ccc} y_{0,0} & y_{1,0} & y_{0,1} & y_{2,0} & y_{1,1} & y_{0,2} \\ \hline y_{1,0} & y_{2,0} & y_{1,1} & y_{3,0} & y_{2,1} & y_{1,2} \\ y_{0,1} & y_{1,1} & y_{0,2} & y_{2,1} & y_{1,2} & y_{0,3} \\ \hline y_{2,0} & y_{3,0} & y_{2,1} & y_{4,0} & y_{3,1} & y_{2,2} \\ y_{1,1} & y_{2,1} & y_{1,2} & y_{3,1} & y_{2,2} & y_{1,3} \\ y_{0,2} & y_{1,2} & y_{0,3} & y_{2,2} & y_{1,3} & y_{0,4} \\ \end{array} \right], \end{equation}
The lines in both matrices indicate various block matrices. Each of these blocks is by itself a Hankel matrix, with the special property that the sum of the data-indices of each element of a block is constant. We call this sum the total degree of the block. The correspondence between the data in a two-dimensional time series and the Vandermonde matrix, containing this data, is shown in Figure~\ref{fig:grid_vandermonde}. The blocks with the same color are blocks containing data with the same total degree.
In general, given a time series \(y_{k,l}\) with \(0\leq k \leq N\) and \(0\leq l \leq N\). The Vandermonde matrix with \(p\) block rows is defined as
\begin{equation*}\label{eqn:VDM_general} \resizebox{.95\hsize}{!}{\( \left[ \begin{array}{c|cc|ccc|c|ccc} y_{0,0} & y_{1,0} & y_{0,1} & y_{2,0} & y_{1,1} & y_{0,2} & \cdots & y_{N-p,0} & \cdots & y_{0,N-p} \\ \hline y_{1,0} & y_{2,0} & y_{1,1} & y_{3,0} & y_{2,1} & y_{1,2} & \cdots & y_{N-p+1,0} & \cdots & y_{1,N-p+1} \\ y_{0,1} & y_{1,1} & y_{0,2} & y_{2,0} & y_{1,2} & y_{0,3} & \cdots & y_{N-p,1} & \cdots & y_{0,N-p} \\ \hline y_{2,0} & y_{3,0} & y_{2,1} & y_{4,0} & y_{3,1} & y_{2,2} & \cdots & y_{N-p+2,0} & \cdots & y_{2,N-p+2} \\ y_{1,1} & y_{2,1} & y_{1,2} & y_{3,1} & y_{2,2} & y_{1,3} & \cdots & y_{N-p+1,1} & \cdots & y_{1,N-p+1} \\ y_{0,2} & y_{1,2} & y_{0,3} & y_{2,2} & y_{1,3} & y_{0,4} & \cdots & y_{N-p,2} & \cdots & y_{0,N-p} \\ \hline y_{0,p} & y_{p+1,0} & y_{p,1} & y_{p+2,0} & y_{p+1,1} & y_{p,2} & \cdots & y_{N,0} & \cdots & y_{p,N-p} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ y_{p,0} & y_{1,p} & y_{0,p+1} & y_{2,p} & y_{1,p+1} & y_{0,p+2} & \cdots & y_{p,N-p} & \cdots & y_{0,N} \\ \end{array} \right] \)} \end{equation*}
From Figure~\ref{fig:grid_vandermonde} we see that there is a problem with the Vandermonde matrix. Not all available data is covered by this matrix. This is a problem for any identification algorithm. When we base our identification solely on the data present in the Vandermonde matrix we are not guaranteed to find a model that suits all available time series data, because it simply disregards part of the available data. In our example, only 60% of the available data is used, counted as the number of unique data elements used in the Vandermonde matrix, divided by the total number of available data. This is addressed in the next section where we introduce the recursive Hankel matrix.
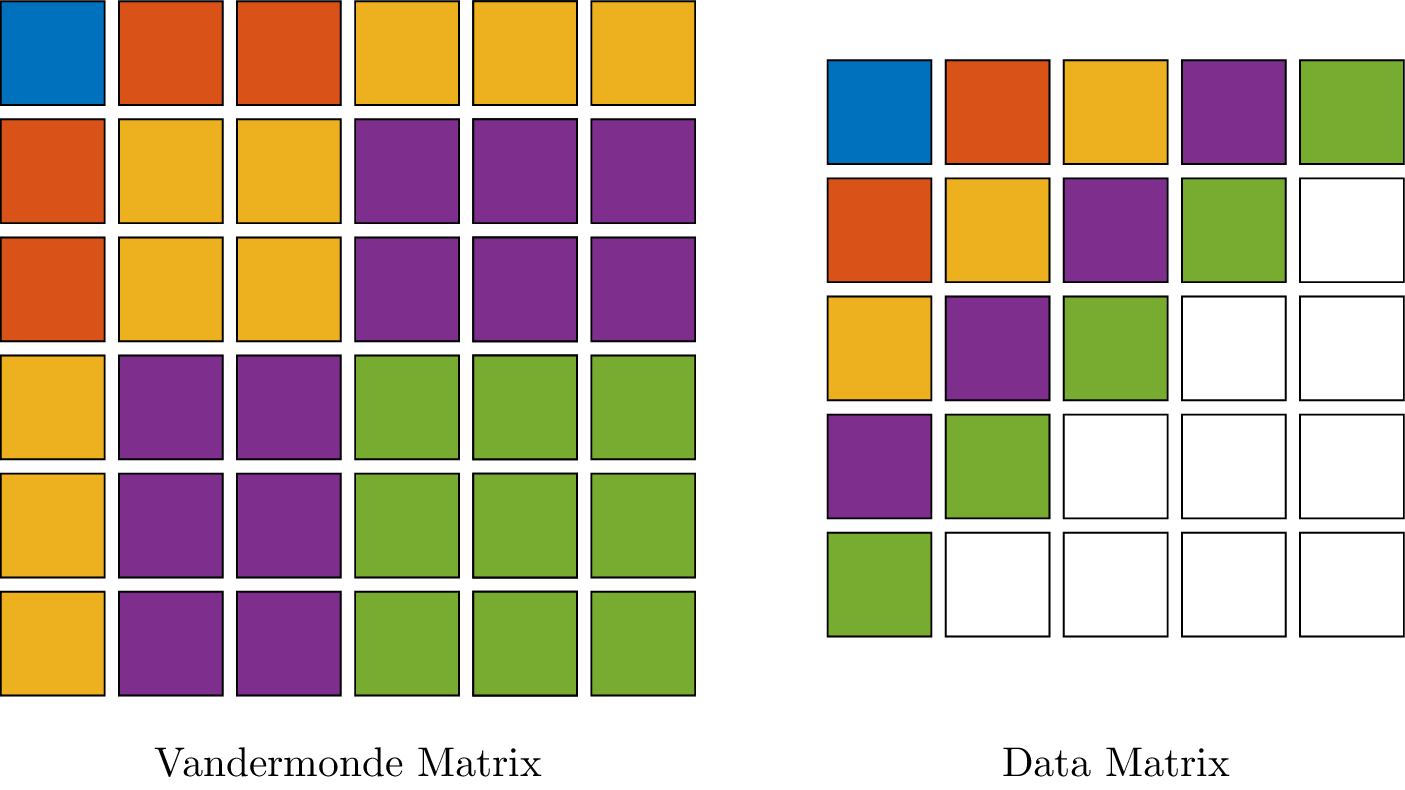
Figure 2: Visual representation of the data correspondence between the Vandermonde matrix and a two-dimensional time series data. The Vandermonde matrix is show on the left side of this figure and a matrix, containing time series data on the right. The colors in both figures correspond to the same data. Every block of the Vandermonde matrix with the same order has the same color and the corresponding data is situated in bands parallel to the anti-diagonal. In this particular example, only 60% of the available time series data is used to construct the Vandermonde matrix. This is calculated by counting the number of colored data points (i.e.~the number of data points that also occur in the Vandermonde matrix), which are 15 points, divided by the total number of data points, which are 25 points.
Recursive Hankel matrix
Using a suitable Hankelization method to incorporate the whole time series is important in any of the identification algorithms presented in the next chapters. Including all data can be achieved by rearranging the rows and column of the Vandermonde matrix. This leads to the introduction of the recursive Hankel matrix. A recursive Hankel matrix, sometimes called a multi-level Hankel matrix~\cite{fasino2000spectral}, is a block Hankel matrix, where every block by itself is a (recursive) Hankel matrix.
Take for example \(y\) to be a two-dimensional time series of size \(3\times3\), indicated below by a matrix populated with the values \(y_{i,j}\). The subscript \((i,j)\) in this notation is the multi-index of the data sample and
\begin{equation}\label{eqn:data-3-by-3} \begin{tikzpicture}[auto,baseline=(current bounding box.east), node distance=1.3cm] \node [draw=none, name=top] { \( y = \begin{bmatrix} {y}_{0,0} & {y}_{0,1} & {y}_{0,2} \\ {y}_{1,0} & {y}_{1,1} & {y}_{1,2} \\ {y}_{2,0} & {y}_{2,1} & {y}_{2,2} \\ \end{bmatrix}. \) }; \end{tikzpicture} \end{equation}
The recursive Hankel matrix \(Y_{0|1,0|1}\) containing the time series \(y\) is equal to
\begin{equation}\label{eqn:RH_example} Y_{0|1,0|1} = \left[ \begin{array}{cc|cc} {y}_{0,0} & {y}_{1,0} & {y}_{0,1} & {y}_{1,1} \\ {y}_{1,0} & {y}_{2,0} & {y}_{1,1} & {y}_{2,1} \\ \hline {y}_{0,1} & {y}_{1,1} & {y}_{0,2} & {y}_{1,2} \\ {y}_{1,1} & {y}_{2,1} & {y}_{1,2} & {y}_{2,2} \\ \end{array} \right]. \end{equation}
The subscript notation of \(Y\) i.e.~\((0|1,0|1)\), denotes the index range over which the index of the data in the first column varies. A subscript \((0|p_1-1,0|p_2-1)\) means that the first element of the first column of the recursive Hankel matrix is equal to \(y_{0,0}\) and the last element of the first column is \(y_{p_1-1,p_2-1}\), this notation is similar as for the definition of the extended recursive observability matrix. All data elements \(y_{k,l}\) with \(0\leq k \leq p_1-1\) and \(0\leq l \leq p_2-1\) are contained in the first column. When the system has only a single output, the matrix \(Y_{0|p_1-1,0|p_2-1}\) has \((p_1 p_2)\) rows. For systems with \(q\) outputs, the recursive Hankel matrix \(Y_{0|p_1-1,0|p_2-1}\) has \(qp_1p_2\) rows.
The recursive Hankel matrix has the structure of a Hankel-block-Hankel matrix~\cite{soton273002} (as indicated by the lines). In other words, a block Hankel matrix with all blocks being Hankel themselves. We conclude that the matrix \(Y_{0|1,0|1}\) can be written as
\begin{equation} Y_{0|1,0|1} = \begin{bmatrix} Y_{0|1,0} & Y_{0|1,1} \\ Y_{0|1,1} & Y_{0|1,2} \\ \end{bmatrix}, \end{equation}
where,
\begin{equation} Y_{0|p-1,i} = \begin{bmatrix} y_{0,i} & y_{1,i} & \cdots & y_{N-p+1,i} \\ y_{1,i} & y_{2,i} & \cdots & y_{N-m+2,i} \\ \vdots & \vdots & \ddots & \vdots \\ y_{p-1,i} & y_{p,i} & \cdots & y_{N,i} \\ \end{bmatrix}. \end{equation}
In some way the matrix \(Y_{0|p-1,i}\) is a partially Hankelized matrix. The first index of the time series data is Hankelized, but the second index stays constant.
It is also important to note that the construction of the recursive Hankel matrix in two dimensions depends on two parameter, which determine the number of rows of the recursive Hankel matrix. This is an important distinction between the recursive Hankel matrix and the Vandermonde matrix. In contrast, the size of the Vandermonde matrix is only determined by a single parameter \(p\), which indicates the total degree of the largest block present in the first row of this matrix.
Definition of the recursive Hankel matrix
The formal definition of the recursive Hankel matrix goes as follows.
Consider an $n-$dimensional data set \(y[k_{1},\cdots,k_{n}] \in \real^{q}\), i.e.~the output of a $n$-dimensional system with \(q\) output. Every value of the index \(k_i\) satisfies \(0\leq k_i \leq N_i\). The recursive Hankel matrix, for this time series, is defined using \(n\) recursions. First the matrix \(Y_{0|p_{1}-1,i_{2},\cdots,i_{n}}\) is defined as
\begin{align} Y_{0|p_{1}-1,i_{2},\cdots,i_{n}} = \begin{bmatrix} y_{0,i_{2},\cdots,i_{n}} & y_{1,i_{2},\cdots,i_{n}} & \cdots & y_{N_1-p_1+1,i_{2},\cdots,i_{n}} \\ y_{1,i_{2},\cdots,i_{n}} & y_{2,i_{2},\cdots,i_{n}} & \cdots & y_{N_1-p_1+2,i_{2},\cdots,i_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ y_{p_1-1,i_{2},\cdots,i_{n}} & y_{p_{1},i_{2},\cdots,i_{n}} & \cdots & y_{N_{1},i_{2},\cdots,i_{n}} \\ \end{bmatrix}. \end{align}
The parameter \(p_{1}\) is a user defined value and influences the number of rows of the recursive Hankel matrix. This is a Hankel matrix where only the first index of the data changes, all other indices are kept constant. The matrix \(Y_{0|p_{1}-1,i_{2},\cdots,i_{n}}\) has dimensions \((qp_{1}) \times (N_{1}-p_{1}+2)\) for every value of the multi-index \((i_{2},\cdots,i_{n})\). The recursive Hankel matrix \(Y_{0|p_{1}-1,0|p_{2}-1\cdots,0|p_{n}-1}\) is recursively defined as
\begin{equation} \label{eqn:rh} \begin{bmatrix} Y_{0|p_{1}-1,0|p_{2}-1,\cdots,0} & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,1} & \cdots & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,N_{n}-p_n+1} \\ Y_{0|p_{1}-1,0|p_{2}-1,\cdots,1} & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,2} & \cdots & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,N_{n}-p_n+2} \\ \vdots & \vdots & \ddots & \vdots \\ Y_{0|p_{1}-1,0|p_{2}-1,\cdots,p_{n}-1} & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,p_{n}} & \cdots & Y_{0|p_{1}-1,0|p_{2}-1,\cdots,N_{n}} \\ \end{bmatrix}. \end{equation}
The size of this matrix is equal to
\begin{equation} q\left(\prod_{i=1}^{n} p_{i} \right) \times \left(\prod_{i=1}^{n} N_{i}-p_{i}+2 \right). \end{equation}
In the recursion step \(k\) the number of rows is chosen to be equal to \(p_{k}\). The set \((p_{1},p_{2},\cdots,p_{n})\) is called the order of the Hankelization.
Alternatively the recursive Hankel matrix can also explicitly be defined as a coordinate mapping. This definition is particularly useful when implementing the recursive Hankel matrix as it serves as a direct formula to calculate the data indices in the matrix. Consider an $n-$dimensional data set \(y[k_{1},\cdots,k_{n}] \in \real^{q}\), i.e.~the output of a $n$-dimensional system with \(q\) outputs. The recursive Hankel matrix is defined as
\begin{equation} Y_{0|p_{1}-1,\cdots,0|p_{n}-1}[i,j] = y[\alpha(i) + \beta(j)], \end{equation}
where the function \(\alpha(i)\) and \(\beta(j)\) are $n-$dimensional coordinate mappings
\begin{equation} \alpha(i) = \left[\alpha_1(i),\cdots,\alpha_{n}(i) \right], \hspace{.2cm} \beta(j) = \left[\beta_{1}(j),\cdots,\beta_{n}(j) \right]. \end{equation}
With,
\begin{equation}\label{eqn:alpha_dit} \alpha_{k}(i) = \left\lfloor \dfrac{i}{\prod\limits_{l=1}^{k-1}p_{l}} \right\rfloor \text{mod}\, (p_{k}) \end{equation}
and,
\begin{equation}\label{eqn:beta_dit} \beta_{k}(j) = \left\lfloor \dfrac{j}{\prod\limits_{l=1}^{k-1}N_{l}-p_{l}+2} \right\rfloor \text{mod}\, (N_{k}-p_{k}+2). \end{equation}
The variables \(p_{k}\) are user defined parameters and determine the number of rows of the recursive Hankel matrix.
The coordinate mappings look complicated at first but they result from the recursive nature of this Hankel matrix, where the modulo operator cycles trough the data coordinates. It is clear that in both Equation~\eqref{eqn:alpha_dit} and Equation~\eqref{eqn:beta_dit} the denominator in the floor operator increases for larger values of \(k\), because it is a product of \(k\) strictly positive integers. With this in mind we formally state that the coordinate \(\alpha_{k}(i)\) changes faster as a function of \(i\) for smaller values of \(k\). This also applies to \(\beta_{k}(i)\). These complicated coordinate mappings are often encountered in research involving tensor structures and tensor unfoldings~\cite{de2000multilinear}.
Example of a small recursive Hankel matrix
To provide some insight in the formulas from Equation~\eqref{eqn:alpha_dit} and Equation~\eqref{eqn:beta_dit}, we provide a small example where \(q=1\), \(p_1=p_2=p_3=2\) and \(N_1=N_2=N_3=2\), i.e.~we preform a Hankelization of order (2,2,2) on a data set of size \(3\times3\times3\) with a single output. The function \(\alpha(i)\) is than equal to
\begin{equation} \alpha(i) = \begin{bmatrix} \alpha(i)_1 & \alpha(i)_2 & \alpha(i)_3 \end{bmatrix} = \begin{bmatrix} i \, \text{mod}\, 2 & \left\lfloor \dfrac{i}{2} \right\rfloor \text{mod}\, 2 & \left\lfloor \dfrac{i}{4} \right\rfloor \text{mod}\, 2 \end{bmatrix} \end{equation}
The data index of the first column of the recursive Hankel matrix is than equal to
\begin{equation} \begin{bmatrix} y_{0,0,0} & y_{1,0,0} & y_{0,1,0} & y_{1,1,0} & y_{0,0,1} & y_{1,0,1} & y_{0,1,1} & y_{1,1,1} \end{bmatrix}^T \end{equation}
From this example, we can see that the first index in the data changes fastest. To make this even more clear, we made the index bold when it changes
\begin{equation} \begin{bmatrix} y_{0,0,0} & y_{\mathbf{1},0,0} & y_{\mathbf{0},\mathbf{1},0} & y_{\mathbf{1},1,0} & y_{\mathbf{0},\mathbf{0},\mathbf{1}} & y_{\mathbf{1},0,1} & y_{\mathbf{0},\mathbf{1},1} & y_{\mathbf{1},1,1} \end{bmatrix}^T \end{equation}
The number of times the first, second and last index changes are respectively \(7,3\) and \(1\).
A sliding window
We can visualize the process of creating a recursive Hankel matrix in a similar way as for the one-dimensional case, depicted in Figure~\ref{fig:Hankel_window_1d}. The proposed Hankelization method is visualized for a two-dimensional time series data in Figure~\ref{fig:Hankel_window_2d}. The time series is depicted on the left side of the image. Every dot in the image represents a measurement or data point ordered on a regular grid. The two-dimensional time series is indexed by two integer values \(k_{1}\) and \(k_{2}\), each variable can for example represent time or a spatial dimension. A rectangular window depicted on the left figure slides over the time series data, following the doted line. Every position of the window corresponds to a column in the recursive Hankel matrix. In the example of Figure~\ref{fig:Hankel_window_2d} a window of size \(2\) by \(2\) is sliding over the time series data. With a time series of size \(5\) by \(6\), the total number of positions the window can be in is \(4 \times 5\). This results in a recursive Hankel matrix of dimension \(4 \times 20\).
The window first slides in the direction indicated with \(k_1\), every step it makes, this index changes, while \(k_2\) stays constant. When the window reaches the end, its position changes with one step in the direction of \(k_2\) and \(k_1\) is set back to zero. This demonstrates the same idea as Equations~\eqref{eqn:alpha_dit} and~\eqref{eqn:beta_dit}. The index \(k_1\) is updated in every column, whereas the index \(k_2\) is updated in every \(4\) steps (counting the initial position of the window as the first step).
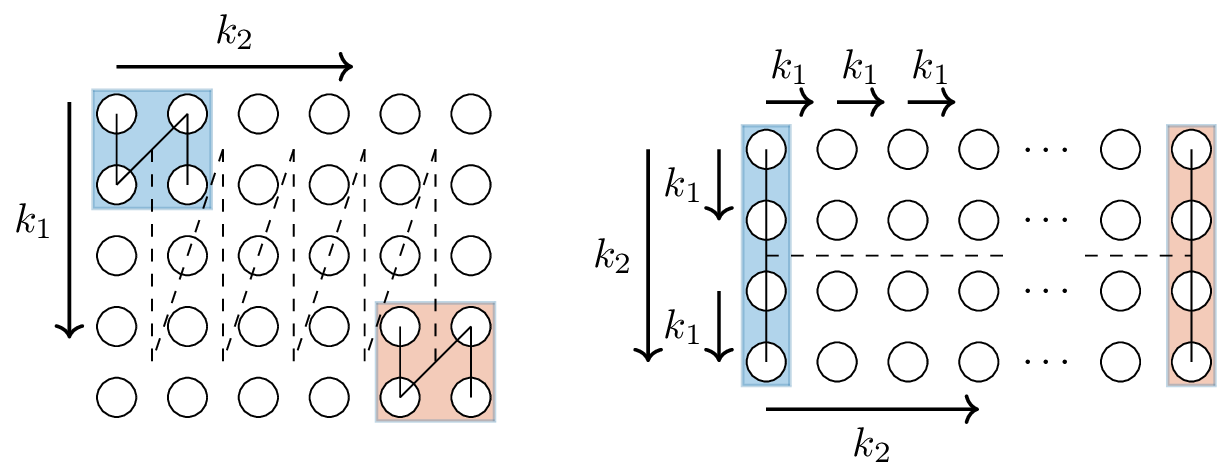
Figure 3: Illustration of the Hankelization method in two dimensions. The left part of this image depicts a two-dimensional time series. Every dot is a data point which are indexed by two integers (k_{1}) and (k_{2}). A window, indicated by a box, slides over the data set, first in the direction of (k_{1}) until the end of the time series data. Next it jumps one column to the right to increase the index of (k_{2}). Every position of the window corresponds to a column in the recursive Hankel matrix. In this particular case the size of the time series data is (5) by (6), there are a total of (4) times (5) possible positions to place the window. The resulting recursive Hankel matrix is shown in the right part of the image and has a size of 4 by 20. The two boxes in the left and right figures correspond to the same position in the data matrix.
Relation between Vandermonde and recursive Hankel matrix
Both the Vandermonde matrix and the recursive Hankel matrix are related to each other. Consider an example with a 2-dimensional time series data of size 4 by 4. This data is equal to the matrix
\begin{equation}\label{eqn:data-example-44} y = \begin{bmatrix} y_{0,0} & y_{0,1} & y_{0,2} & y_{0,3} \\ y_{1,0} & y_{1,1} & y_{1,2} & y_{1,3} \\ y_{2,0} & y_{2,1} & y_{2,2} & y_{2,3} \\ y_{3,0} & y_{3,1} & y_{3,2} & y_{3,3} \\ \end{bmatrix}. \end{equation}
We will first construct a Vandermonde matrix with the available data. This matrix is equal to
\begin{equation}\label{eqn:VDM} V = \left[\begin{array}{c|cc|ccc} y_{0,0} & y_{1,0} & y_{0,1} & y_{2,0} & y_{1,1} & y_{0,2} \\ \hline y_{1,0} & y_{2,0} & y_{1,1} & y_{3,0} & y_{2,1} & y_{1,2} \\ y_{0,1} & y_{1,1} & y_{0,2} & y_{2,1} & y_{1,2} & y_{0,3} \\ \hline y_{2,0} & y_{3,0} & y_{2,1} & \multicolumn{3}{c}{\multirow{3}{*}{\raisebox{-2mm}{\scalebox{3}{$\times$}}}} \\ y_{1,1} & y_{2,1} & y_{1,2} \\ y_{0,2} & y_{1,2} & y_{0,3} \end{array}\right]. \end{equation}
The big \(\times\) in the matrix indicates a missing block. There is no data available to construct this block of the Vandermonde matrix. The largest square Vandermonde matrix that can be constructed from a time series data of size 4 by 4 has therefor only size 3 by 3. We can however work with a tall or fat version of the Vandermonde matrix. The tall matrix contains the first 3 columns of the matrix in Equation~\eqref{eqn:VDM} and has 6 rows, whereas the fat matrix contains the first 3 rows of the matrix in Equation~\eqref{eqn:VDM} and has 6 columns.
We can also construct the recursive Hankel matrix from the data in Equation~\eqref{eqn:data-example-44}. When using a window of size \(3\times3\), corresponding to a Hankelization of order \((3,3)\), we get the following recursive Hankel matrix
\begin{equation} Y_{0|2,0|2} = \left[ \begin{array}{cc|cc} y_{0,0} & y_{1,0} & y_{0,1} & y_{1,1} \\ y_{1,0} & y_{2,0} & y_{1,1} & y_{2,1} \\ y_{2,0} & y_{3,0} & y_{2,1} & y_{3,1} \\ \hline y_{0,1} & y_{1,1} & y_{0,2} & y_{1,2} \\ y_{1,1} & y_{2,1} & y_{1,2} & y_{2,2} \\ y_{2,1} & y_{3,1} & y_{2,2} & y_{3,2} \\ \hline y_{0,2} & y_{1,2} & y_{0,3} & y_{1,3} \\ y_{1,2} & y_{2,2} & y_{1,3} & y_{2,3} \\ y_{2,2} & y_{3,2} & y_{2,3} & y_{3,3} \\ \end{array} \right]. \end{equation}
This tall matrix has size 9 by 4. It is interesting to note that the tall Vandermonde matrix can be constructed from the recursive Hankel matrix by rearranging the columns and rows. Row and column permutations can be represented by matrix multiplications, this leads to the following equality.
\begin{equation} V = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} y_{0,0} & y_{1,0} & y_{0,1} & y_{1,1} \\ y_{1,0} & y_{2,0} & y_{1,1} & y_{2,1} \\ y_{2,0} & y_{3,0} & y_{2,1} & y_{3,1} \\ y_{0,1} & y_{1,1} & y_{0,2} & y_{1,2} \\ y_{1,1} & y_{2,1} & y_{1,2} & y_{2,2} \\ y_{2,1} & y_{3,1} & y_{2,2} & y_{3,2} \\ y_{0,2} & y_{1,2} & y_{0,3} & y_{1,3} \\ y_{1,2} & y_{2,2} & y_{1,3} & y_{2,3} \\ y_{2,2} & y_{3,2} & y_{2,3} & y_{3,3} \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{equation}
The matrices that are pre- and post-multiply with \(Y_{0|2,0|2}\) are respectively of full row and column rank. It follows that the rank of the Vandermonde matrix is smaller than or equal to the rank of the recursive Hankel matrix, generated from the same multi-dimensional time series data.
It can be shown in general that, given a limited set of observations, we can always construct a larger recursive Hankel matrix than a Vandermonde matrix. Because the columns and the rows of the Vandermonde matrix are a subset and permutation of the rows and columns of the recursive Hankel matrix it also follows that the rank Vandermonde matrix will be smaller or equal to the rank of the recursive Hankel matrix constructed from the same multi-dimensional time series data. The rank of both matrices will be important in the next chapters covering realization theory.
Factorization of the recursive Hankel matrix
In this section we calculate the factorization of both the Vandermonde matrix and the recursive Hankel matrix for regular and singular systems.
Regular systems
Substituting the output of a two-dimensional state space model described by \(y_{k,l} = CA^kB^lx\) in the recursive Hankel matrix from Equation~\eqref{eqn:RH_example} results in
\begin{equation} Y_{0|1,0|1} = \left[ \begin{array}{cc|cc} Cx & CAx & CBx & CABx \\ CAx & CA^{2}x & CABx & CA^{2}Bx \\ \hline CBx & CABx & CB^{2}x & CAB^{2}x \\ CABx & CA^{2}Bx & CAB^{2}x & CA^{2}B^{2}x \\ \end{array} \right]. \end{equation}
This matrix can be factorized as the product of two matrices
\begin{equation} Y_{0|1,0|1} = \Gamma_2 X_2 \left[ \begin{array}{c} C \\ CA \\ \hline CB \\ CAB \end{array} \right] \left[ \begin{array}{cc|cc} x & Ax & Bx & ABx \end{array} \right]. \end{equation}
This demonstrates that the recursive Hankel matrix is the outer product of a recursive observability matrix and a recursive state sequence matrix. This result is summarized in the following theorem.
Given an $m-$dimensional time series data \(y[k_1,\cdots,k_m]\in \real^q\), with \(0\leq k_i \leq n_i\), which is the output of a commuting state space model defined by the matrices \((A_1,\cdots,A_m, C)\) and initial state \(x\) such that
\begin{equation} y[k_1,\cdots,k_m] = C A_1^{k_1}\cdots A_m^{k_m} x. \end{equation}
The recursive Hankel matrix \(Y_{0|p_1-1,\cdots,0|p_m-1}\) of order \((p_1,\cdots, p_m)\) which has \(qp_1p_2\cdots p_m\) rows and \((n_1-p_1+2)(n_2-p_2+2)\cdots (n_m-p_m+2)\) columns can be factorized as
\begin{equation} Y_{0|p_1-1,\cdots,0|p_m-1} = \Gamma_m X_m \end{equation}
with,
\begin{equation} \Gamma_{k} = \begin{bmatrix} \Gamma_{k-1} \\ \Gamma_{k-1}{A}_{k} \\ \Gamma_{k-1}{A}_{k}^{2} \\ \vdots \\ \Gamma_{k-1}{A}_{k}^{p_{k}-1} \\ \end{bmatrix} \end{equation}
and
\begin{equation} X_{k} = \begin{bmatrix} X_{k-1} & {A}_{k}X_{k-1} & {A}_{k}^{2}X_{k-1} & \cdots & {A}_{k}^{m_{k}-p_{k}-1}X_{k-1} \end{bmatrix}, \end{equation}
The starting conditions of this recursion relation with \(k=0\) is defined by \(\Gamma_{0} = C\) and \(X_0 = x\).
This factorization follows directly from the definition of the recursive Hankel matrix.
Descriptor systems
A similar factorization result for commuting descriptor systems can be obtained by substituting the solution of descriptor systems in the entries of the recursive Hankel matrix. Given the two-dimensional commuting descriptor system with regular matrix pencils \((A,E)\) and \((B,F)\), where all 4 matrices form a commuting family, output matrix \(C\) and initial state \(x\). Assume that the output of the system is defined for the indices \((k,l)\) with \(0\leq k \leq 2\) and \(0\leq l \leq 2\). In this case, the output is equal to
\begin{equation} y[k,l] = C\mathcal{A}^k_2\mathcal{B}^l_2x = CA^kE^{2-k}B^lF^{2-l}x. \end{equation}
The recursive Hankel matrix from Equation~\eqref{eqn:RH_example} is than
\begin{equation} Y_{0|1,0|1} = \left[\begin{array}{cc|cc} C\mathcal{A}^0_2\mathcal{B}^0_2x & \mathcal{A}^1_2\mathcal{B}^0_2x & \mathcal{A}^0_2\mathcal{B}^1_2x & \mathcal{A}^1_2\mathcal{B}^1_2x \\ C\mathcal{A}^1_2\mathcal{B}^0_2x & \mathcal{A}^2_2\mathcal{B}^0_2x & \mathcal{A}^1_2\mathcal{B}^1_2x & \mathcal{A}^2_2\mathcal{B}^1_2x \\ \hline C\mathcal{A}^0_2\mathcal{B}^1_2x & \mathcal{A}^1_2\mathcal{B}^1_2x & \mathcal{A}^0_2\mathcal{B}^2_2x & \mathcal{A}^1_2\mathcal{B}^2_2x \\ C\mathcal{A}^1_2\mathcal{B}^1_2x & \mathcal{A}^2_2\mathcal{B}^1_2x & \mathcal{A}^1_2\mathcal{B}^2_2x & \mathcal{A}^2_2\mathcal{B}^2_2x \\ \end{array}\right], \end{equation}
which can be factorized as
\begin{equation} Y_{0|1,0|1} = \left[\begin{array}{c} C\mathcal{A}^0_1\mathcal{B}^0_1 \\ C\mathcal{A}^1_1\mathcal{B}^0_1 \\ \hline C\mathcal{A}^0_1\mathcal{B}^1_1 \\ C\mathcal{A}^1_1\mathcal{B}^1_1 \end{array}\right] \left[\begin{array}{cc|cc} \mathcal{A}^0_1\mathcal{B}^0_1x & \mathcal{A}^1_1\mathcal{B}^0_1x & \mathcal{A}^0_1\mathcal{B}^1_1x & \mathcal{A}^1_1\mathcal{B}^1_1x \end{array}\right], \end{equation}
which is the outer product of an extended recursive observability matrix and an extended recursive state sequence matrix for singular systems. This result in generalized in the following theorem for two-dimensional systems.
Given $m-$dimensional time series data \(y[k_1,\cdots,k_m]\in \real^q\), with \(0\leq k_i \leq n_i\), which is the output of a commuting descriptor system defined by the regular matrix pencils \((A_1,E_1),\cdots,(A_m,E_m)\), which form a commuting family, the generalized state \(x\) and output matrix \(C\in\real^q\). The output of the system is
\begin{equation} y[k_1,\cdots,k_m] = C A_1^{k_1}E_1^{n_1-k_1} \cdots A_m^{k_m}E_m^{n_m-k_m} x = C \mathcal{A}_{1,n_1}^{k_1} \cdots \mathcal{A}_{m,n_m}^{k_m} x. \end{equation}
The recursive Hankel matrix \(Y_{0|p_1-1,\cdots,0|p_m-1}\) of order \((p_1,\cdots, p_m)\) which has \(qp_1p_2\cdots p_m\) rows and \((n_1-p_1+2)(n_2-p_2+2)\cdots (n_m-p_m+2)\) columns can be factorized as
\begin{equation} Y_{0|p_1-1,\cdots,0|p_m-1} = \robs_m X_m \end{equation}
with,
\begin{equation} \robs_{k} = \begin{bmatrix} \robs_{k-1} \mathcal{A}_{k,p_k-1}^{0} \\ \robs_{k-1} \mathcal{A}_{k,p_k-1}^{1} \\ \vdots \\ \robs_{k-1} \mathcal{A}_{k,p_k-1}^{p_k-1} \\ \end{bmatrix}, \end{equation}
and
\begin{equation} X_{k} = \begin{bmatrix} X_{k-1} \mathcal{A}_{k,n_k-p_k+2}^{0} & X_{k-1} \mathcal{A}_{k,n_k-p_k+2}^{1} & \cdots & X_{k-1} \mathcal{A}_{k,n_k-p_k+2}^{n_k-p_k+2} \end{bmatrix}. \end{equation}
The starting conditions of this recursion relation with \(k=0\) is defined by \(\Gamma_{0} = C\) and \(X_0 = x\).
Conclusion
In this chapter we presented two methods to Hankelized multi-dimensional time series data; the Vandermonde matrix and the recursive Hankel matrix. The Vandermonde matrix was introduced by calculating the outer product of the observability matrix and the state sequence matrix, whereas the recursive Hankel matrix is the product of the recursive observability and recursive state sequence matrices.
We demonstrated that the Vandermonde matrix is not compatible when working with time series data of a rectangular domain. In this case, nearly 50% of the data can not be incorporated in the Vandermonde structure. This observation lead to the introduction of the recursive Hankel matrix.