Problem statement
Modeling multi-dimensional systems
In recent years increasing attention in system theory is paid to multi-dimensional dynamic systems. These so-called \gls{nD} systems are characterized by signals that depend on several independent variables. These variables can be for example time and space, in which case observations are not only correlated in time, but also in space.
As an example, imagine a bridge or a mechanical structure. At discrete regular locations, sensors are placed that measure the local displacement (or acceleration) of the bridge over time. When sensors are placed over the length and the width of the bridge, we get a two-dimensional plain of sensor. This sensor plain, together with the third dimension of time, records a three-dimensional data set of the movements of the top surface of the bridge in time. One coordinate registers the location length-wise of the sensors, a second coordinate registers the coordinate of the sensor in the width of the bridge and the third coordinate registers the time instance of the measurements. The bridge in this case, together with the sensors, is an example of a discrete multi-dimensional system. Multi-dimensional, because of the location of the sensors, discrete, because we only measure the displacement at a finite number of locations separated in space and time.
In this thesis multi-dimensional systems are represented as commuting state space model or commuting descriptor system, which are direct extensions of one-dimensional state space models and descriptor systems. An overview of the model structure is shown in Table~\ref{tbl:int-models}. When defining a model class we have to be careful that all model properties are well defined and solutions to the model exist. This leads to analysis of a canonical representation which can be used to reduce an arbitrary valid model description in to a well understood canonical representation.
\begin{table}[h] \caption[Overview of the models used in this thesis.]{ Overview of the models used in this thesis. The state vector is indicated by $x$, the system matrices are $A,B,E$ and $F$ and the output matrix is $C$.} \label{tbl:int-models} \centering \begin{tabular}{c|cc} & Regular & Singular \\ \midrule 1D & $\begin{array} {r} \\ x[k+1] = Ax[k] \\ y[k] = Cx[k] \end{array}$ & $\begin{array} {r} \\ Ex[k+1] = Ax[k] \\ y[k] = Cx[k] \end{array}$ \\ 2D & $\begin{array} {r} \\ x[k+1,l] = Ax[k,l] \\ x[k,l+1] = Bx[k,l] \\ y[k,l] = Cx[k,l] \end{array}$ & $\begin{array} {r} \\ Ex[k+1,l] = Ax[k,l] \\ Fx[k,l+1] = Bx[k,l] \\ y[k,l] = Cx[k,l] \end{array}$ \\ \bottomrule \end{tabular} \end{table}
Describing multi-dimensional systems
Defining and proving the existence of a multi-dimensional model class is only half the work. A second challenge is to derive all emergent properties of our newly introduced commuting state space models and descriptor systems. Classical properties like observability and controllability have to be assessed and various tests like the Popov–Belewich–Hautus test have to be extended for the presented classes of state space models. This analysis in turn is based on the canonical representation and the eigenvalues of the involved system matrices.
Another classical results is the link between state space models and difference equations, which heavily relies on the theorem of Cayley–Hamilton. Finding a canonical system representation is important as it determines the most general case for which the presented model classes are still well-posed.
The last problem is to `solve’ the presented models, i.e.~quantify the set of all possible solutions as a function of the involved matrices. This analysis leads to the introduction of the multi-dimensional eigenmodes and the classification of different kind of solutions.
Identifying multi-dimensional systems
After all system properties have been analyzed, we tackle the problem of deriving a suitable identification algorithm, starting from a multi-dimensional time series and obtaining a multi-dimensional state space model.
The first challenge lies in the involved matrix structures, one-dimensional systems are estimated using a Hankel matrix. This matrix can be extended in two different ways to incorporate multi-dimensional data. Both methods are studied and compared.
In Figure \ref{fig:prediction-subspace} two classes of methods are presented, on the one side we have the class of prediction error methods~\cite{ljung2002prediction} and on the other side the class of subspace methods~\cite{van1994n4sid}. This thesis focuses on subspace methods where the observable time series data is reshaped in a so called Hankel matrix and the fundamental (sub) spaces of this Hankel matrix are then used to calculate a suitable model realization.
![Figure 1: [Comparison between subspace methods and prediction error methods.] Comparison between subspace methods and prediction error methods. With prediction error methods, first the model parameters are estimated, and only in a second phase the state. In subspace identification the identification steps are switched, the state sequence is estimated first, which effectively linearizes the problem.](/subspacepem.png)
Figure 1: [Comparison between subspace methods and prediction error methods.] Comparison between subspace methods and prediction error methods. With prediction error methods, first the model parameters are estimated, and only in a second phase the state. In subspace identification the identification steps are switched, the state sequence is estimated first, which effectively linearizes the problem.
State of the art
In this section we provide an overview of the existing theory for representing and identifying multi-dimensional systems. The presented algorithm and ideas covered in this thesis are based on root finding algorithms, which we adapt for the purpose of system identification.
Root finding and systems identification
Univariate root finding
At the basis of linear systems theory lies the root finding problem. Given a univariate polynomial
\begin{equation} p(x) = p_0 + p_1x + p_2x^2 + \cdots + p_nx^n = 0 \end{equation}
with some order \(n\) and constants \(p_i\), find all values of \(x\) that satisfy this equation. An overview of the methods for solving this problem is provided in~\cite{pan1997solving}.
Linear state space models are linked to univariate polynomials via the theorem of Cayley–Hamilton~\cite{mertzios1986generalized}, which states that a square matrix satisfies its own characteristic equation.
Multivariate root finding and the Macaulay matrix
Similar to the one-dimensional case, root finding plays an important role in multi-dimensional system theory. The extended theorem of Cayley–Hamilton for sets of commuting matrices~\cite{mertzios1986generalized} relates commuting state space models to a set of multivariate polynomials.
Algorithms and methods for finding solution of multivariate polynomial equations can largely be placed in two categories, algebraic methods, for example algorithms based on a Gr\“obner basis~\cite{buchberger1965algorithmus} and algorithms based on linear algebra~\cite{faugere1994resolution,dreesen2013back}. This last category of techniques uses Macaulay-like matrices~\cite{vermeersch2019globally} for solving polynomial systems. The Macaulay matrix is matrix which contains the polynomial coefficients in a certain order. The null space of this matrix is span by a generalized Vandermonde matrix~\cite{press1992numerical}, which can be linked in a natural way to a data matrix containing multi-dimensional time series.
Solutions at infinity
Both one-dimensional and multi-dimensional polynomial systems can have solutions at infinity. One-dimensional dynamic systems can model solutions at infinity with so called descriptor systems~\cite{luenberger1978time}. Descriptor systems are also sometimes called differential-algebraic equations~\cite{petzold1982differential} or \gls{DAE}’s. As the name implies, this subset of systems are a combination of differential equations equipped with algebraic constrains. Specific identification algorithms for this class of one-dimensional systems exist in the literature~\cite{moonen1992subspace}.
A generalization of descriptor systems for multi-dimensional systems has been used before in the context of roots at infinity and is referred to as `mind the gap’~\cite{dreesen2013back}. This gap has not yet been analyzed in details and no attempts have been made in the past to thoroughly study multi-dimensions descriptor systems.
Existing multi-dimensional systems
Parallel to the one-dimensional case, nD system representations can be categorized in three main groups, rational transfer function representations, local state space representations and a behavioral realization. The first group of rational transfer function models correspond to the class of the multivariate rational functions. By applying a series of integral transformations to a partial differential equation (e.g. Laplace transformation, Fourier transformation,…) these models can easily be constructed.
The second class of local state space models for two-dimensional systems (with straightforward generalizations to nD systems) have been proposed by Roesser, Attasi, Fornasini, Marchesini, and Kurek (see e.g.~references in~\cite{galkowski2001state,zerz2000topics}. The behavioral approach~\cite{willems1987time,willems1986timea,willems1986timeb} to nD systems has been initiated by Rocha and Willems~\cite{rocha2011markovian}.
Existing realization methods
Realization algorithms can be divided in two categories, on the one hand we have the class of prediction error methods and on the other hand the class of subspace methods. Both realization algorithm are shown in Figure~\ref{fig:prediction-subspace}.
With prediction error methods, first the model parameters are estimated, which in general is a nonlinear non-convex problem, and only in a second phase, when needed, a (Kalman) filter or observer is used to estimate the states. In subspace identification the identification steps are switched: the state sequence is estimated first, which effectively linearizes the problem. Once the state has been estimated, all other unknown quantities, such as the system matrices and output matrix can be estimated via a linear least squares estimation.
An overview of subspace methods for one-dimensional systems is given by Van Overschee~\cite{van1994n4sid}. In his work deterministic and stochastic identification methods are discussed. The deterministic identification algorithms are based on the algorithm of Kung~\cite{kung1978new}, which uses the shift invariant structure of the extended observability matrix. The shift invariant property can be extended to multi-shift invariant matrix spaces~\cite{de2021multiparameter}.
A simple example
The one-dimensional heat equation
The classic `textbook’ example of a multi-dimensional system is the one-dimension heat equation, which is an example of a partial differential equation~\cite{strauss2007partial}. The one-dimension heat equation describes the temperature evolution on an ideal one-dimensional surface, like a thin metal rod. This process is described by
\begin{equation} \dfrac{\partial T}{\partial t} = \dfrac{\partial^2 T}{\partial x^2}, \end{equation}
where \(T\) is the temperature, \(t\) is the time an \(x\) is the location on the one-dimensional surface. The two independent variables, space and time, make this a two-dimensional problem. To keep this example as simple as possible, we will work with dimensionless variables, and describe the solution for the surface \(0\leq x\leq 1\) and \(0\leq t \leq 1\).
To fully describe the problem, the initial temperature distribution and the boundary conditions must be specified. The boundary conditions are a description of the behavior of the solution at the boundaries of the physical domain. Two common conditions are the homogeneous Dirichlet boundary condition, where the temperature at the boundary is kept constant to zero, and the homogeneous Neumann boundary condition, where the temperature flux is set to zero. This last condition represents a perfectly insulating boundary, where no energy transport is possible.
In this example we use a set of homogeneous Dirichlet conditions, which can be specified as
\begin{equation} \begin{aligned} T(t,0) = T(t,1) = 0, & ~\forall~0\leq t \leq 1. \end{aligned} \end{equation}
As the initial condition for our particular problem, we use
\begin{equation} T(0,x) = T_0(x) = \begin{cases} 2x & 0\leq x\leq 0.5,\\ 2(1-x)& 0.5 < x \leq 1. \end{cases} \end{equation}
To find a solution for this particular problem we use the well-known technique of separation of variables~\cite{haberman1983elementary} and write the proposed solution as a product of two univariate functions
\begin{equation} T(t,x) = U(t)V(x). \end{equation}
By plugging in this solution into the partial differential equation we find
\begin{equation} U(t)‘V(x) = U(t)V(x)’’, \end{equation}
which can be rewritten as
\begin{equation} \frac{U(t)’}{U(t)} = -c^2 = \frac{V(x)’’}{V(x)}. \end{equation}
Because the left part of the equation only depends on \(t\) and the right part of the equation only depends on \(x\), both expressions must be constant. As per convention in the literature this constant value is indicated by \(-c^2\), the reason for this convention will become clear in the next step of the derivation. The use of separation of variables has reduced the partial differential equation to a set of two coupled ordinary differential equations, namely
\begin{equation} \begin{aligned} U(t)’ = & -c^2 U(t), \\ V(x)’’ = & -c^2 V(x), \end{aligned} \end{equation}
which both have known solutions
\begin{equation} \begin{aligned} U(t) = & c_1 e^{-c^2t}, \\ V(x) = & c_2 \sin(cx) + c_3 \cos(cx). \end{aligned} \end{equation}
This solution still depends on the constants \(c_1,c_2,c_3\) and \(c\) which are obtained by using the boundary conditions and the initial condition.
From the first boundary condition \(T(t,0) = 0\) we know that \(V(0) = c_3 \cos(0) = 0\), which is only the case when \(c_3\) is 0. By using the second boundary condition \(T(t,1) = 0\) we have that \(V(1) = c_2 \sin( c) = 0\) which is only true if \(c\) is a multiple of \(\pi\), i.e.~\(c=n\pi\) for some natural number \(n\). This shows that
\begin{equation} T(t,x)_n = \alpha_n e^{-(n\pi)^2t}\sin(n\pi x), \end{equation}
is a valid solution which satisfies the boundary condition for all values of \(\alpha_n\) and all natural numbers \(n\). Because the heat equation, with constant coefficients, is an example of a linear partial differential equation~\cite{treves1975basic} we also have that all linear combinations of solutions are a solution, and
\begin{equation}\label{eqn:int-example-four} T(t,x) = \sum_{n=0} \alpha_n e^{-(n\pi)^2t}\sin(n\pi x). \end{equation}
The last step is to find the right coefficients \(\alpha_n\) for which the initial condition is matched. This can be done by using Fourier analysis~\cite{howell2016principles}. In this example we only use the first 5 non-zero terms in the sum of Equation~\eqref{eqn:int-example-four}. This solution is shown in Figure~\ref{fig:int-example-solution}
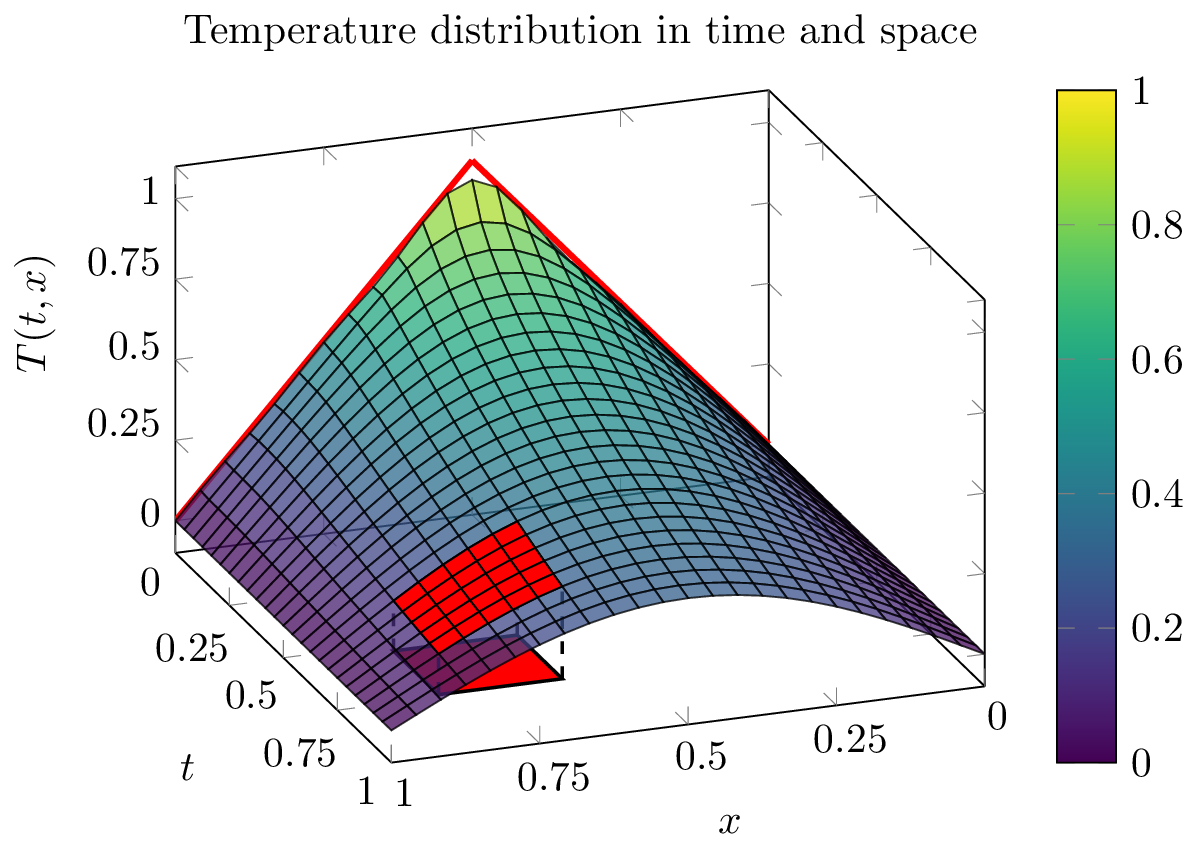
Figure 2: A plot of the solution of the heat equation used in this example. The red line at (t=0) represents the ideal initial condition. To keep the order of the state space model finite, we only use the first 5 non-zero eigenmodes to compute an approximate solution to the specified initial condition. The red patch is a small selection of (6times 6) data points with form the columns off the recursive Hankel matrix, used to calculate a system realization.
The discretized solution
The presented theory in this thesis involves discrete systems, we thus need to transform the continuous solution in Equation \eqref{eqn:int-example-four} to a discrete alternative. Take \(N_x\) the number of discretization points in space, which are equidistantly spaced over the closed interval \([0,1]\) and \(N_t\) is the number of equidistantly sampled points in time over the closed interval \([0,1]\). This makes the total number of measurements equal to \(N_x \times N_t\). The discrete solution for \(0\leq k\leq N_t-1\) and \(0\leq l \leq N_x-1\) is
\begin{equation}\label{eqn:int-example-four-two} T[k,l] = \sum_{n=0} \alpha_n e^{\frac{-(n\pi)^2k}{N_t-1}}\sin(\frac{n\pi l}{N_x-1}). \end{equation}
Without going into much details for now, we can write a single element of this sum as the output of a two-dimensional commuting state space model. This commuting state space model is given by
\begin{equation} \begin{aligned} x[k+1,l] = & \begin{bmatrix} e^{\frac{-(n\pi)^2}{N_t-1}} & 0 \\ 0 & e^{\frac{-(n\pi)^2}{N_t-1}} \end{bmatrix}x[k,l] \\ x[k,l+1] = & \begin{bmatrix} \cos(\frac{n\pi}{N_x-1}) & \sin(\frac{n\pi}{N_x-1}) \\ -\sin(\frac{n\pi}{N_x-1}) & \cos(\frac{n\pi}{N_x-1}) \end{bmatrix}x[k,l] \\ T_n[k,l] = & \begin{bmatrix} 0 & \alpha_n \end{bmatrix} x[k,l], \end{aligned} \end{equation}
and the initial state \(x[0,0] = [1,0]^T\). The solution to this state space model is \(T_n[k,l] = C A^kB^lx[0,0]\), where \(A\) is the square matrix in the first model equation, \(B\) is the square matrix in the second model equation and \(C\) is the output matrix, relating the state vector \(x\) and the output of the system. To verify the solution we have that
\begin{eqnarray*} T_n[k,l] = \begin{bmatrix}0 & \alpha_n\end{bmatrix} \begin{bmatrix} e^{\frac{-(n\pi)^2k}{N_t-1}} & 0 \\ 0 & e^{\frac{-(n\pi)^2k}{N_t-1}} \end{bmatrix} \begin{bmatrix} \cos(\frac{n\pi l}{N_x-1}) & \sin(\frac{n\pi l}{N_x-1}) \\ -\sin(\frac{n\pi l}{N_x-1}) & \cos(\frac{n\pi l}{N_x-1}) \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \end{eqnarray*}
which is the same expression as given in Equation \eqref{eqn:int-example-four-two}.
This analysis shows that the discretized solution of the heat equation can be modeled by the class of commuting state space models. The specific techniques for doing so are not discussed in this thesis as continuous partial differential equations are not covered.
Estimating the heat equation
We have just shown that the discrete solution of the one-dimensional linear heat equation can be modeled using the class of commuting state space models, which is the topic op this thesis. A second question that we can ask is: \textit{Is it possible to estimate the system dynamics, based on observed data?} In this case we start with two-dimensional time series data of size \(N_t \times N_x\) and we would like to identify the commuting state space model
\begin{equation} \begin{aligned} x[k+1,l] = & A x[k,l] \\ x[k,l+1] = & B x[k,l] \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
such that \(y[k,l]\) matches the observed data. In order to do this we will first reshape the observed data into a so-called recursive Hankel matrix, which will be introduced later in this thesis. The idea is to identify the linear relations between adjacent data points by rearranging the data as the rows of the recursive Hankel matrix. This process is shown in Figure \ref{fig:int-example-solution}, where the red patch in the plot is a region of \(6\times 6\) points, which are selected and reshaped as the rows of a matrix. In total, for a data set of size \(25\times 25\) we can select 400 such regions\footnote{Computed as $20\times 20$. 6 consecutive points can be selected at 20 positions in a set of 25 points. If we do this for two dimensions, we end up with a total of 400 possible arrangements.}. The recursive Hankel matrix is the collection of all 400 vectorized regions and has a size of \(400\times 36\). The linear relations between the columns of this matrix correspond to the linear relations between the data points in the two-dimensional time series. We will later demonstrate that the recursive Hankel matrix can be factorized as the outer product of an extended recursive observability and extended recursive state sequence matrix. Both matrices are then used to estimate the systems dynamics.
Research objectives and contributions
System descriptions and well-posedness conditions
In total this thesis covers 4 different classes of state space models which are represented in Table~\ref{tbl:int-models}. One-dimensional system theory is well understood by now and not much can be added to the field of autonomous state space models. However in this thesis we present a generalization of the analysis of one-dimensional descriptor systems. Classically this model class is described by using the Weierstrass canonical form (\gls{WCF}), which is tedious to compute and work with. Extending the \gls{WCF} to multi-dimensional systems is also far from trivial, but a generalization, suitable for multi-dimensional descriptor systems, has been derived in this thesis. Instead we explore descriptor system where all system matrices commute, every well-posed descriptor system can be transformed to this form. Using this assumption, we have simplified the framework and even found a small mistake in the existing literature.
After presenting one-dimensional systems we start by introducing their multi-dimensional counterpart, the commuting state space model and the commuting descriptor system. Both system representations are already studied and used in the context of polynomial root finding~\cite{dreesen2013back} but not all system properties are well understood. The main contribution here is the derivation of the well-posedness condition for multi-dimensional commuting descriptor systems. In the past the class of descriptor systems were only indirectly obtained as a byproduct of a root finding algorithm but no general criteria existed to describe the entire model class. We will show that the commutativity of the model matrices is an important property to describe this model class.
Derived system properties and modal solutions
The known textbook-theory for one-dimensional state space models has been extended to include multi-dimensional commuting state space models and descriptor systems. Firstly the theorem of Cayley–Hamilton was extended to a family of commuting matrices. This result was then further used to derive a set of difference equations which are related to the state space model. The theorem of Cayley–Hamilton was also the key component to extend the observability matrix and Kalman criteria for multi-dimensional systems.
Analyzing descriptor systems is more complicated, as no pre-existing well-posedness criteria existed. It was not clear under which conditions a model had a solution or when it did not. After proving a general well-posedness condition a multitude of results where derived for this model class. Most notably the proof and classification of different kinds of solutions at infinity, together with the derivation of a suitable theorem of Cayley–Hamilton.
The canonical representation of multi-dimensional commuting state space models and descriptor systems allows us to derive an expression for the eigenmodes, i.e.~the collection of all solutions, of these models. For the commuting states space model, this derivation is largely based on the Schur’s lemma, to calculate the shared eigenvectors of the system matrices. The analysis for descriptor systems is a bit more involved, and is largely based on the existence of a canonical model form. This canonical form reveals the structure of the solutions of a descriptor system, for which we have demonstrated, can have multiple different types of solutions, based on the eigenvalues structure of the involved system matrices.
Realization theory
Understanding multi-dimensional systems is only half the work, the goal is to derive a suitable realization algorithm to obtain the system matrices, and the state sequence based on observed output data. The first challenge was to find a method to incorporate all data in the identification process, as previous established techniques based on the Macaulay matrix where not suitable for the task at hand. We overcame this issue by defining the recursive Hankel matrix. The properties of this matrix are analyzed by the theorem of Cayley–Hamilton which in term relies heavily on the canonical system representation.
Something that came as a surprise was the description of the observability for multi-dimensional descriptor systems. Previously these systems had only been studied in the context of root-finding algorithm, and the solutions at infinity where never explicitly considered. In this thesis we discover a complex structure hidden in the solutions of this model class and show that the classical observability matrix, is not suitable to asses the observability of commuting descriptor systems.
Another well known concept concerning realization of descriptor systems is the phrase `Mind the gap’. In this thesis, the so called gap will be studied and two realization algorithms are presented, both for one-dimensional systems and for multi-dimensional systems. One of these algorithms for one-dimensional descriptor systems is novel and does not require the complex calculations of the gap. Similar, for multi-dimensional systems, two algorithms are presented, one algorithm where a gap calculation is required and one algorithm without the gap calculation.
Finally the partial realization condition for both commuting state space models and for commuting descriptor systems is derived.
Approach taken in this thesis
To tackle the problem of multi-dimensional subspace identification, we will combine two important ideas developed at ESAT in the last two decades. On the one hand we start from a model description, which we call the commuting state space model, that was previously studied by Dreesen in his thesis on polynomial room finding~\cite{dreesen2013back}. The second work that lies at the basis of our research endeavor is the work done by Van Overschee on subspace identification~\cite{van2012subspace}. Both theories are founded in applied numerical linear algebra. This is the language that will be used to describe and tackle the problem finding a suitable intersection between these two field.
In the first part of this thesis we discuss and derive the model properties of autonomous commuting state space models and commuting descriptor systems. We will be looking at the parallels (and differences) between one-dimensional system theory and the multi-dimensional extension.
The main properties of autonomous commuting state space model are related to the eigenvalues of the system matrices, which must commute in order for the model to be well posed. This commutation is a key factor and we will spend a lot of time investigating the properties of commuting matrices. An important result of the first part of this thesis, and which is the driver for a lot of system properties, is the existence of a generalized eigenbasis for a set of commuting system matrices~\cite{horn2012matrix}. Understanding this eigenbasis is of paramount importance for the derivation of the properties of the commuting state space model. With this result we will derive a modal decomposition of the output of autonomous commuting state space models. This modal decomposition has the same structure as the discretized form of the know analytic solution of certain partial differential equations, like the heat equation and wave equation.
In the next research phase, the study of commuting matrices is extended to the framework of linear matrix pencils~\cite{Ikramov1993}. A matrix pencil is a linear map that is defined by two square matrices, both of which can be singular. This branch of linear algebra is concerned about the generalized eigenvalue problem, where the eigenvalues and eigenvectors depend on both matrices of the matrix pencil. Dreesen showed in his thesis \cite{dreesen2013back} that the generalized eigenvalues of a matrix pencil can model solutions at infinity. From a system theoretical perspective these solutions correspond to non-causal behavior of the system. We will investigate these non-causal effects and the implications on the model class. The previous condition where the system matrices must commute becomes non-trivial when working with matrix pencils. Commutativity, in the classical sense, is no longer defined. Its a challenging task to define the correct set of criteria on a set of matrix pencils such that the multi-dimensional descriptor system is well defined. In this study we extensively use the theory of the Weierstrass canonical form~\cite{kalogeropoulos2008weierstrass}. To our best knowledge, this has never been studied in this way before.
The second part of this thesis covers the realization problem of commuting state space models. This part is mostly inspired by the work done by Van Overschee presented in his thesis and book~\cite{van2012subspace}. The algorithms presented by Van Overschee are based around the factorization and the properties of Hankel matrix. This matrix is a structured matrix, containing the observed (input-) output data. The Hankel structure is not directly compatible with a multi-dimensional framework. In this work we explored two methods to extend the concept of Hankelization (i.e. the method of creating a Hankel matrix form observed data) and compare both. The first matrix structure which can be regarded as an extension of the Hankel matrix to multiple dimensions is called the Vandermonde matrix~\cite{horn2012matrix}. This structure was previously extensively used in the work done by Dreesen, however in the context of system identification this matrix has some flaws. The analysis of the Vandermonde matrix leads to the introduction of a second extension of the Hankel matrix called the recursive Hankel matrix~\cite{kazeev2013multilevel,fasino2000spectral}. A part of the realization theory of Van Overschee is then rewritten using this matrix instead of the classical Hankel matrix.
Overview per chapter
This thesis has is divided in three main parts;
- Part \ref{p:one} covers existing one-dimensional system theory.
- In Part \ref{p:two}, multi-dimensional systems are introduced and their properties studied.
- The last part, Part \ref{p:three}, covers realization theory of one-dimensional and multi-dimensional systems.
The next chapter, \textbf{Chapter~\ref{ch:linear-algebra}} introduces some fundamental concepts of linear algebra which are extensively used in this thesis.
One-dimensional regular state space models are introduced in \textbf{Chapter~\ref{ch:1DR}}. The concepts like the observability and state sequence matrices are introduced for this class of systems. This chapter serves as a brief overview of system theory and is mainly used as an introduction to guide the reader in the next chapters.
In \textbf{Chapter~\ref{ch:1DS}}, one-dimensional descriptor systems are introduced, together with the concept of the generalized state. This chapter also introduced the Weierstrass canonical form and matrix pencils and illustrates the challenges when working with matrix pencils.
The next chapter, \textbf{Chapter~\ref{ch:2DR}}, introduces the class of two-dimensional commuting state space models. We start this chapter by demonstrating the importance of the commutativity of the system matrices, if the systems matrices do not commute, the model is not well-posed. This commutation constraint opens the door to use the theory of commuting matrices to study the eigenvalues and the properties of this model class. We finally introduce the theorem of Cayley–Hamilton for commuting matrices, which allows us to define the state sequence and observability matrices for the class of commuting state space models.
In \textbf{Chapter~\ref{ch:2DS}} commuting state space models are extended to commuting descriptor systems, by introducing two extra system matrices. The first part of this chapter is dedicated to proving the well-posedness of this model class, which is far from trivial. The well-posedness condition is necessary to calculate a canonical from which in turn allows us to describe the model class in the most general case. In this chapter we also reveal the intricate structure of the non-causal and causal solutions which can be produced as the output of a commuting descriptor system.
After describing 4 model classes we finally start to focus on the identification problem for multi-dimensional state space models by generalizing the Hankel matrix in \textbf{Chapter~\ref{ch:hankel}}. In total two possible generalizations are provided, the recursive Hankel matrix and generalized Hankel matrix. Both matrices can be factorized, and the factorization can be linked to the observability and state sequence matrices. The presented generalization of the Hankel matrix will form the basis of the realization algorithm presented in the next chapters.
The number of dimensions in reduced again in \textbf{Chapter~\ref{ch:1real}} as we will briefly cover one-dimensional realization theory. This chapter introduces all basic notions like a shift-invariant subspace and the partial realization theorem.
Finally we arrive at \textbf{Chapter~\ref{ch:2real}} where we introduce the realization problem for two-dimensional commuting state space models and two-dimensional commuting descriptor systems. In total we present two algorithms for the realization problem for two-dimensional commuting state space models, one with a so called `gap’ and one without. The later algorithm can also be used in general to identify regular commuting state space models. We conclude this chapter by proving the partial realization condition for regular and descriptor systems. The last part of this chapter covers the realization problem for higher dimensional commuting state space models and descriptor systems.
The conclusions of this thesis are summarized in~\textbf{Chapter~\ref{ch:conclusion}}.