State space model
This thesis is focused around the state space representation of linear time invariant systems. A regular one-dimensional autonomous state space model is described by
\begin{equation}\label{eqn:1R-SS} \begin{aligned} x[k+1] = & A x[k] \\ y[k] = & C x[k]. \end{aligned} \end{equation}
The matrix \(A \in \real^{m\times m}\) is called the system matrix and the matrix \(C \in \real^{q\times m}\) the output matrix. The state vector is denoted by the vector \(x \in \real^m\). The first equation is called the state update equation, updating the state at every index \(k\), whereas the second equation is the output equation, relating the internal state and the output. In this thesis we use the shorthand notation \((C,A)\) to refer to this state space model. Unless stated differently, the matrix \(A\) is always used as the system matrix and the matrix \(C\) is always used as the output matrix of the state space model. An autonomous state space model has no input affecting the state, the output is thereby completely determined by the initial state of the model denoted by \(x[0]\). Systems and quantities indexed by square brackets, are discrete valued, meaning that the state vector \(x[k]\) only exist for the discrete values \(k\in \N\). On the other hand, systems and quantities indexed by parentheses are functions with a continuous independent variable.
State sequence
Starting from the initial state and using the system equations of the state space model we can derive an expression for the output of a state space model. This expression is obtained by recursively using the state update equation of the state space model in Equation~\eqref{eqn:1R-SS}. In this way we have
\begin{equation} x[1] = A x[0],~x[2] = Ax[1] = A^2x[0],~\cdots~,~x[k] = A^k x[0]. \end{equation}
By using the output equation we find that
\begin{equation} y[k] = C x[k] = C A^k x[0], \end{equation}
We will analyze the solutions of this expression in Section~\ref{sec:1d_modal} when discussing the modal solution of a state space model.
The theorem of Cayley–Hamilton
The output of a state space model is determined by the eigenvalues of the system matrix and its characteristic polynomial. To demonstrate this we first introduce the theorem of Cayley–Hamilton.
The square complex matrix \(A\) of size \(m \times m\) satisfies its own characteristic equation as defined by
\begin{equation}\label{eqn:char_poly_thm_ch} p(z) = \det(z\eye-A) = z^m + \alpha_1 z^{m-1} + \dots + \alpha_m \end{equation}
such that \(p(A) = 0\).
The result of Cayley–Hamilton has some important implications in system theory, most notably when calculating the difference equation associated to a state space model and when analyzing the observability of a linear state space model.
To illustrate the theorem of Cayley–Hamilton, we provide a small example. Consider the following 3 by 3 matrix
\begin{equation}\label{eqn:nogeenmatrix} A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end{bmatrix}. \end{equation}
The characteristic polynomial of this matrix is equal to \(p(z) = \det(z\eye-A) = z^3 - 4 z^2 + 5z -2\). It is easy to verify that the matrix \(A\) indeed satisfies this relation and that \(A^3 - 4A^2+5A-2\eye = 0\).
The theorem of Cayley–Hamilton implies that for every matrix \(A\) of size \(m\times m\) there exist a positive integer \(p\) such that \(A^p\) becomes linearly dependent to the set of matrices \(\{A^0,A^1,\cdots, A^{p-1}\}\). This theorem provides an upper bound for the value of \(p\) which is always smaller than or equal to \(m\). The lower bound on this value is discussed in Section~\ref{sec:1R_minimal} which introduces the minimal polynomial of a square matrix.
Difference equation
Linear dynamical systems can also be represented by difference equations~\cite{kailath1980linear}. An autonomous shift invariant finite order difference equation is given by
\begin{equation}\label{eqn:diff-1d} y[k+m] = - (\alpha_1 y[k+m-1] + \dots + \alpha_m y[k]). \end{equation}
The difference equation is parameterized by \(m\) coefficient \(\alpha_1, \alpha_2, \dots, \alpha_m\), where \(\alpha_m\) can not be equal to zero. The order of a difference equation is equal to the longest lag present in the equation, which is \(m\) in this case.
Every difference equation can be linked to a characteristic polynomial by introducing the shift operator $D$~\cite{jordan1965calculus}, which, as the name implies, shifts a time series \(y[k]\) by a single lag, such that \(Dy[k] = y[k+1]\). The difference equation from Equation~\eqref{eqn:diff-1d} can be transformed by using the shift operator to
\begin{equation} \left(D^m + \alpha_1 D^{m-1} + \dots + \alpha_m \right) y[k] = 0. \end{equation}
The polynomial \(p(x) = \left(x^m + \alpha_1 x^{m-1} + \dots + \alpha_m \right )\) is called the characteristic polynomial of the difference equation. The order of this polynomial is the same as the order of the linear difference equation.
Difference equations and state space models are related to each other. A linear system can be transformed from a linear state space model to a difference equation and the other way around. Transforming a state space model to a difference equation is done via the theorem of Cayley–Hamilton, which was presented in Section~\ref{sec:1R-CH}. For a given state space model \((C,A)\) with initial state \(x[0]\) we first calculate the characteristic polynomial of the system matrix as \(p(z) = \det(z\eye-A) = z^m + \alpha_1 z^{m-1} + \dots + \alpha_m\). When we multiply \(p(A)\) from the left and right respectively by \(C\) and the state \(A^k x[0]\) we get
\begin{multline} C(A^m + \alpha_1 A^{m-1} + \dots + \alpha_m)A^k x[0] = \\ CA^{m+k}x[0] + \alpha_1 CA^{m-1+k}x[0] + \dots + \alpha_m CA^{k}x[0] = 0. \end{multline}
By using the formula for the output of a state space model, that is \(y[k] = CA^k x[0]\), we get
\begin{equation} y[m+k] = - (\alpha_1 y[m-1+k] + \dots + \alpha_m y[k]). \end{equation}
This shows that the coefficients of the difference equation associated to a state space model \((C,A)\) are equal to the coefficients of the characteristic equation of the system matrix. Note that the output matrix of a state space model does not affect the characteristic polynomial. The influence of the output matrix on the difference equation is discussed in Section~\ref{sec:1R_minimal}.
The other way around, computing a state space realization for a given difference equation is done via realization theory or by using the companion matrix~\cite{horn2012matrix} associated to the characteristic polynomial of the difference equation. All systems with system matrix
\begin{equation}\label{eqn:1R_companion} A = \begin{bmatrix} 0 & 0 & \dots & 0 & \alpha_{m} \\ 1 & 0 & \dots & 0 & \alpha_{m-1} \\ 0 & 1 & \dots & 0 & \alpha_{m-2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & 1 & \alpha_{{1}} \end{bmatrix} \end{equation}
satisfy
\begin{equation}\label{eqn:1R_diff_for_companion} y[m+k] = - (\alpha_1 y[m-1+k] + \dots + \alpha_m y[k]) \end{equation}
for any given output matrix and initial state. The matrix in Equation~\eqref{eqn:1R_companion} is the companion matrix of the difference equation from Equation~\eqref{eqn:1R_diff_for_companion}. Both system representations and the methods to transform one form in to the other are summarized in Figure~\ref{fig:1R-relation-ss-dif}.
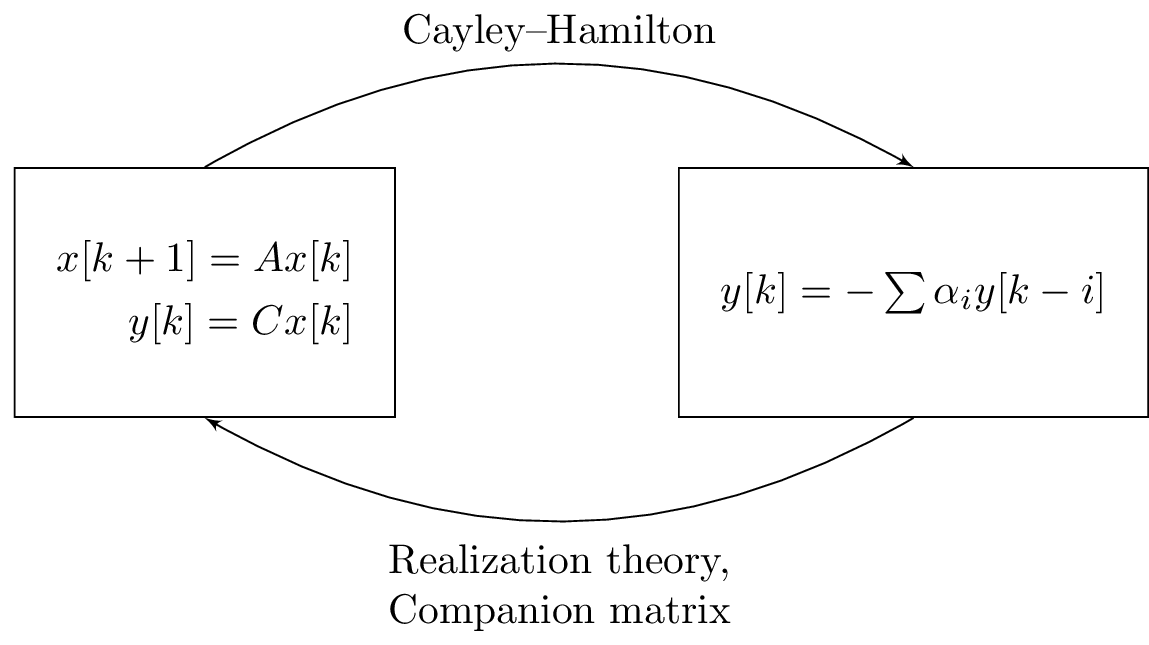
Figure 1: Linear systems can be represented via a state space model and a difference equation. Transforming a state space model to a difference equation is done via the theorem of Cayley–Hamilton, while the reverse transformation is done by using either realization theory or the companion matrix of the difference equation.
Minimal polynomial
The theorem of Cayley–Hamilton states that there always exists a polynomial with the same degree as the number of columns/rows of a square matrix such that \(p(A) = 0\). However, the theorem does not state that this polynomial is the minimal polynomial, i.e.~the unique monic polynomial of minimal degree. A trivial example where the minimal polynomial differs from the characteristic polynomial is the identity matrix of size \(m\times m\), here denoted by \(A\). The characteristic polynomial of this matrix is
\begin{equation}\label{eqn:zero_derogatory} p(z) = \det(z\eye - A) = \det \left( \begin{bmatrix} z-1 & 0 & \dots & 0 \\ 0 & z-1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & z-1 \\ \end{bmatrix} \right)= (z-1)^m. \end{equation}
It is clear that \((A-\eye)^m\) is equal to zero but so is \(A-\eye\), implying that the characteristic polynomial is not of minimal degree. In this case, the minimal polynomial has degree 1 and is equal to \(p(z) = z-1\). From this analysis we can introduce a new polynomial, namely the minimal polynomial of a square matrix.
The minimal polynomial of a square matrix \(A\) is defined as the monic polynomial \(p(z)\) of minimal degree such that \(p(A)=0\).
The minimal polynomial always exists and is unique, its degree is bound by the theorem of Cayley–Hamilton.
Observability
``Assume the system to be observable’’, this sentence is probably one of the most used expressions in the literature covering systems theory. The concept of observability was first introduced by Kalman~\cite{kalman1960new,kalmanLinear} for the class of differential equations. Loosely speaking, a system is observable when it is possible to observe/estimate the internal representation of the system based on a finite set of observations from the system. This internal representation of the system is indicated by its state.
Kalman devised a test to check the observability for the class of linear state space models. This test is directly based on the construction of the observability matrix, which relates the internal state to the output of the system. With his test, Kalman proved that, if and only if, this matrix is of full rank, the system is observable. This test however, only provided a `yes’ or `no’ answer, it did not quantify `how observable’ a system is. The results of Kalman implicitly depend on the theorem of Cayley–Hamilton. This theorem ensures that the rank of the observability matrix stabilizes after a finite number of observations.
A first attempt at quantifying exactly how observable a system is, was formulated by Brown~\cite{brown1966not}. His research lead to the introduction of the degree of observability for linear state space models~\cite{Ablin1967}.
In the years following the description of observability by Kalman, an additional criterion to determine the observability of a linear systems was devised, which is referred to as the Popov–Belevitch–Hautus test~\cite{popov1973hyperstability} or \gls{PBH}-test for short. This test is based on the Hautus lemma~\cite{hautus1969controllability} and gives an answer to exactly which eigenmodes of the system are (un-)observable. In this section, both ideas of Kalman and Hautus are discussed and in later chapters extended to the multi-dimensional case.
Estimating the internal state
The concept of observability of dynamic systems was first introduced by Kalman, he wrote~\cite{kalmanLinear}: a linear autonomous dynamical system is completely observable at time \(t_0\) if it is not algebraically equivalent, for all \(t \leq t_0\), to any system of the type
\begin{align} & \dfrac{dx_1}{dt} = F^{11}(t)x_{1}(t), \\ & \dfrac{dx_2}{dt}= F^{21}(t)x_{1}(t) + F^{22}(t)x_{2}(t), \\ & y(t) = H^{1}(t)x_{1}(t). \end{align}
Two state vectors are indicated with \(x_1(t)\) and \(x_2(t)\). The system matrices \(F^{ij}\) can in general be time varying. In this representation, the output of the system only depends on the values of the state \(x_1(t)\). The state \(x_2(t)\) does not affect the output of the system. It is thus impossible to reconstruct, or observe, the complete state vector consisting of the states \(x_1(t)\) and \(x_2(t)\), solely based on measurements of the output \(y(t)\). The part of the state vector that is un-observable is \(x_2(t)\). This is further illustrated in Figure~\ref{fig:observability_scheme}.
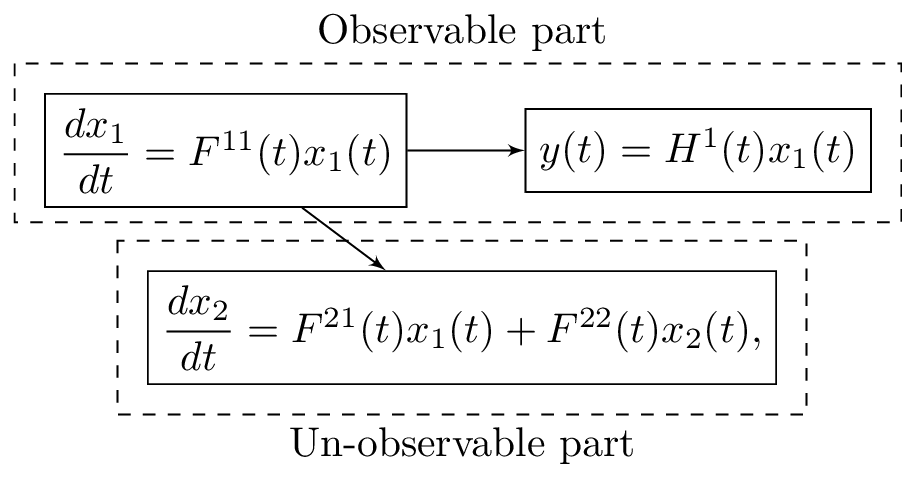
Figure 2: Schematic representation of the observability of a system. The entire state of the system is indicated by the collection of (x_1(t)) and (x_2(t)). The output (y(t)) of the system is not affected by the value of the state vector (x_2). This makes it impossible to estimate/observe the value of the state vector (x_2) based on measurements of the output signal.
The observability matrix
Two equivalent theorems for observability regarding state space models have been proven in the past. The first one by Kalman goes as follows.
The state space model from Equation~\eqref{eqn:1R-SS} with \(q\) outputs and a $m$-dimensional state vector is observable if and only if the observability matrix is of full rank. The observability matrix is given by
\begin{equation} \obs = \begin{bmatrix} C^T & (CA)^T & \dots & (CA^{m-1})^T \end{bmatrix}^T. \end{equation}
The number of block rows that form this matrix is equal to \(m\), which is the dimension of the state vector. The size of the matrix is \(qm\times m\).
The presented observability matrix \(\obs\) relates the internal state of the system and the output. Take the first \(m\) outputs \(y[0],y[1],\cdots, y[m-1]\) of a state space model \((C,A)\) with initial state \(x[0]\). We have that
\begin{equation} \begin{bmatrix} y[0] \\ y[1] \\ \vdots \\ y[m-1] \end{bmatrix} = \begin{bmatrix} C \\ CA \\ \vdots \\ CA^{m-1} \end{bmatrix} x[0] = \obs x[0]. \end{equation}
If and only if the observability matrix is of full rank, the value of the initial state can be estimated. Expanding the observability matrix to include more rows of the form \(CA^n\) with \(n>m-1\) will not increase the rank of \(\obs\) due to the theorem of Cayley–Hamilton. This proofs Theorem \ref{thm:1DR-kalman-obs}.
Popov–Belevitch–Hautus
A second condition to guarantee the observability of a state space model is called the Popov–Belevitch–Hautus test~\cite{belevitch1968classical,popov1973hyperstability}.
The state space model from Equation~\eqref{eqn:1R-SS} with \(q\) outputs and an $m$-dimensional state vector is observable if and only if the \((q+m)\times m\) dimensional matrix
\begin{equation} \begin{bmatrix} A- \lambda \eye \\ C \end{bmatrix} \end{equation}
has rank \(m\) for all possibly complex values of \(\lambda\).
It has been proven in~\cite{hautus1969controllability} that both criteria are equivalent. Theorem~\ref{thm:1DR-kalman-obs} and Lemma~\ref{thm:1DR-hausus} describe, and test, the observability fundamentally in a different way. The result formulated in Lemma~\ref{thm:1DR-hausus} tells us something more than just whether or not the system is observable. It also tells us which eigenvalues/eigenmodes of the system are (un-)observable. Whenever one of the eigenvectors of the system matrix \(A\) is orthogonal to the row-space of the output matrix, the system becomes un-observable.
Non-observable systems and column compressions
When a system is non-observable, it is possible to calculate the observable part. This is done in an algorithm called a column compression and uses the singular value decomposition of the rank-deficient observability matrix. Assume that the observability matrix indicated by \(\obs\), for the state space model \((C,A)\) has rank rank \(r\) strictly smaller than \(m\). By calculating the singular value decomposition of the observability matrix we get
\begin{equation} U \Sigma V^T = \obs. \end{equation}
Because the observability matrix is not of full rank the singular values can be split in two sets and we get
\begin{equation} U \Sigma V^T = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix}. \end{equation}
The matrix \(\Sigma_0\) is a diagonal matrix with strictly positive real elements on the diagonal. A property of the singular value decomposition is that the number of non-zero elements on the diagonal of \(\Sigma\) is equal to the rank of the matrix. A state space model is uniquely defined up to a basis transformation. This means that both state space models \((C,A)\) and \((CV,V^TAV)\), where \(V\) is the right singular matrix of the observability matrix, are the same state space models. We can now construct the observability matrix for this transformed state space model. This matrix is indicated by \(\obs_V\) and we get the following equality
\begin{equation} \obs_V = \begin{bmatrix} CV \\ CAV \\ \vdots \\ CA^{n-1}V \end{bmatrix} = \obs V. \end{equation}
By using the singular value decomposition of the original observability matrix \(\obs\) we find and expression for \(\obs_V\) which is equal to
\begin{equation} \obs_V = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix} \begin{bmatrix} V_0 & V_1 \end{bmatrix} = \begin{bmatrix} U_0 \Sigma_0 & 0 \end{bmatrix}. \end{equation}
This result follows immediately from the fact that right singular matrix is an orthonormal matrix. In this basis, the observability matrix has only \(r\) non-zero columns, this explains the term column compression. The column space has been compressed and reduced to a smaller set of linearly independent vectors.
A Column compression allows us to define a new state space model which is observable and has a lower order \(r\). Because the first row of the observability matrix is equal to the output matrix \(CV\), it follows that \(CV = \begin{bmatrix} C_0 & 0\end{bmatrix}\). We now partition the transformed system matrix \(V^TAV\) as
\begin{equation} V^TA V = \begin{bmatrix} A_{0,0} & A_{0,1} \\ A_{1,0} & A_{1,1} \end{bmatrix}. \end{equation}
The product between \(CV\) and \(V^TAV\) is then equal to
\begin{equation}\label{eqn:observability_1} CVV^TA V = \begin{bmatrix} C_0 & 0\end{bmatrix} \begin{bmatrix} A_{0,0} & A_{0,1} \\ A_{1,0} & A_{1,1} \end{bmatrix} = \begin{bmatrix} C_0A_{0,0} & C_0A_{0,1}\end{bmatrix} = \begin{bmatrix} C_0A_{0,0} & 0 \end{bmatrix}. \end{equation}
The last equality follows directly from the fact that the \(CVV^TA V\) is the second block-row of the compressed observability matrix, which has only \(r\) non-zero columns. Repeating this recursions \(m-1\) times up to and including the term \(CV(V^TA V)^{m-1}\) we find an expression for the compressed observability matrix which is equal to
\begin{equation} \obs_V = \begin{bmatrix} C_0 & 0 \\ C_0A_{0,0} & 0 \\ \vdots & \vdots \\ C_0 A_{0,0}^{m-1} & 0 \end{bmatrix}. \end{equation}
This is the observability matrix of the state space model \((C_0,A_{0,0})\) appended by \(m-r\) zero vectors. We can also conclude that the block \(A_{0,1}\) is identically equal to zero.
Every state space model \((C,A)\) can thus be transformed to
\begin{equation} C = \begin{bmatrix} C_0 & 0 \end{bmatrix}, A = \begin{bmatrix} A_{0,0} & 0 \\ A_{1,0} & A_{1,1} \end{bmatrix} \end{equation}
where the subsystem \((C_0,A_{0,0})\) is observable.
This derivation presents an algorithm to calculate an observable system \((C_0,A_{0,0})\) starting from the non-observable system \((C,A)\) by eliminating the non-observable states using the singular value decomposition of the observability matrix. In the next section we will present the controllability property of a state space model in a similar way. Combining both results of observability and controllability allows us to calculate the minimal realization of a state space model using the Kalman decomposition.
Controllability
The state sequence matrix
Parallel to observability, we can define the notion of controllability. Classically controllability is reserved for systems with an input term. In the autonomous case however, we only focus on the initial state, denoted by \(x[0]\). Instead of defining a controllability matrix, we instead define the state sequence matrix. This matrix, as the name implies, contains a sequence of states, starting from the initial state \(x[0]\) up to and including \(x[m-1]\). For the state space model \((C,A)\), the state sequence matrix is equal to
\begin{equation} X = \begin{bmatrix} x[0] & x[1] & \dots & x[m-1] \end{bmatrix} = \begin{bmatrix} x[0] & Ax[0] & \dots & A^{m-1}x[0] \end{bmatrix}. \end{equation}
A linear state space model is controllable if and only if its state sequence matrix is of full rank.
Row compressions
When a state space model is non-controllable the state sequence matrix will be rank deficient and we can preform a row compression on this matrix. Consider the non-observable state space model \((C,A)\) and define the state sequence matrix \(X\). We calculate the singular value decomposition of this matrix to find the row space and the rank of the state sequence matrix. In this way we get
\begin{equation} X = U \Sigma V^T = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix}. \end{equation}
Similar to the analysis of observability, we introduce a new equivalent state space model \((CU, U^TAU)\) which only differs by a change of basis from \((C,A)\). By changing the basis, we change the initial state to \(z[0] = U^T x[0]\). In this basis, the state sequence matrix, now denoted by \(Z\), becomes
\begin{equation} Z = \begin{bmatrix} U^Tx[0] & U^TAx[0] & \cdots & U^TA^{n-1}x[0] \end{bmatrix} = U^T X. \end{equation}
Using the singular value decomposition of the state sequence matrix \(X\) we find that
\begin{equation} Z = U^T U \Sigma V^T = \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix} = \begin{bmatrix} \Sigma_0 V_0^T \\ 0 \end{bmatrix}. \end{equation}
The state sequence matrix is transformed as
\begin{equation} U^T X = \begin{bmatrix} z_0[0] & z_0[1] & \cdots & z_0[m-1] \\ 0 & 0 & \cdots & 0 \\ \end{bmatrix}. \end{equation}
Every state space model \((C,A)\) can thus be transformed to
\begin{equation} C = \begin{bmatrix} C_0 & C_1 \end{bmatrix}, A = \begin{bmatrix} A_{0,0} & A_{0,1} \\ 0 & A_{1,1} \end{bmatrix}, z[0] = \begin{bmatrix} z_0[0] \\ 0 \end{bmatrix}, \end{equation}
where the subsystem \((C_0,A_{0,0})\) with initial state \(z[0]\) is controllable.
Extended observability and state sequence matrices
A generalization of both the observability and the state sequence matrices are respectively the extended observability and extended state sequence matrices. Both matrices are characterized by an order, which respectively denotes the number of block row or block columns the extended observability or extended state sequence matrices have. Consider the state space model \((C,A)\) which has order \(m\). The extended observability matrix of order \(m\) is the same as the observability matrix. Similarly, the extended state sequence matrix of order \(m\) is the same as the state sequence matrix of the system.
The extended observability matrix of order \(n\) is denoted as \(\obs_{0|n-1}\). The subscript indicates the range of the powers of the system matrix as it occurs in the blocks of \(\obs_{0|n-1}\), i.e.~the first block is \(C\) and the last block is \(CA^{n-1}\). We have
\begin{equation} \obs_{0|n-1} = \begin{bmatrix} C \\ CA \\ \vdots \\ CA^{n-2} \\ CA^{n-1} \end{bmatrix}. \end{equation}
The same convention is used for the extended state sequence matrix which is denoted by \(X_{0|n-1}\) and is equal to
\begin{equation} X_{0|n-1} = \begin{bmatrix} x[0] & x[1] & \cdots & x[n-1] \end{bmatrix}. \end{equation}
Kalman decomposition
In the previous two sections, we demonstrated a method to calculate the observable and the controllable parts of a linear state space model. When combing both techniques we can calculate 4 subsystems;
- a system that is controllable and observable,
- a system that is controllable but not observable,
- a system that is observable but not controllable,
- and a system which is neither controllable nor observable.
This system decomposition is called the Kalman decomposition~\cite{kalmanLinear}.
Calculating the minimal realization
The minimal realization of a state space model is the part of a system that is controllable and observable. We already showed how to calculate the observable part in Section~\ref{sec:1R-colcomp} and the controllable part in Section~\ref{sec:1R-rowcomp}. By combining both calculations, we can find the part of the state space model that is observable and controllable. To calculate the minimal realization, we first calculate \((C_0,A_{0,0})\) which is the observable part of the state space model \((C,A)\). Starting from the system \((C_0,A_{0,0})\) we then calculate the controllable part of this system. The resulting system is the minimal realization of \((C,A)\).
Calculating the Kalman decomposition
The steps to calculate the Kalman decomposition follow the same line as the calculation of the minimal realization of a state space model. The numerical details are presented in~\cite{boley1984computing}.
The Kalman decomposition of the state space model \((C,A)\) is equal to the system \((CT^{-1},TAT^{-1})\) where
\begin{equation}\label{eqn:1R_kalman} T^{-1}= \begin{bmatrix} T_{co} & T_{\overline{c}o} & T_{c\overline{o}} & T_{\overline{co}} \end{bmatrix}. \end{equation}
The four submatrices are
- The columns of \(T_{co}\) form a basis for the observable and controllable part of the system.
- The columns \(T_{\overline{c}o}\) form a basis for the observable but non-controllable part of the system.
- The columns \(T_{c\overline{o}}\) form a basis for the controllable but non-observable part of the system.
- The columns \(T_{\overline{co}}\) form a basis for the part of the system that is neither controllable nor observable.
These four matrices are obtained by calculating the singular value decomposition of the state sequence matrix and the observability matrix. Denote the left singular vectors of the observability matrix by \(\begin{bmatrix} U_0 & U_1 \end{bmatrix}\) and the left singular vector of the state sequence matrix by \(\begin{bmatrix} H_0^T & H_1^T\end{bmatrix}\), for the system \((C,A)\) with state vector \(x\in \real^m\). The matrices \(U_0\) and \(H_0\) form an orthonormal basis of the column space of respectively the observability matrix and the state sequence matrix. As shown in~\cite{boley1984computing}, the four submatrices from Equation~\eqref{eqn:1R_kalman} are calculated by
- \(T_{co}\) is the projection of \(U_0\) on \(H_0\).
- \(T_{\overline{c}o}\) is the projection of \(U_0\) on the orthogonal complement of \(H_0\), in this case denoted by \(H_1\).
- \(T_{c\overline{o}}\) is the projection of the orthogonal complement of \(U_0\), which is \(U_1\) on \(H_0\).
- \(T_{\overline{co}}\) is the projection of the orthogonal complement of \(U_0\) on the orthogonal complement of \(H_0\).
Modal analysis
The output of a one-dimensional state space model can be written as the linear combination of eigenmodes of the system. This is called the modal analysis. Two cases are discussed. In the first case, we assume that the system matrix can be diagonalized. In the second case, we drop this assumption and a general system matrix is considered.
Diagonalizable case
Consider a one-dimensional autonomous state space model \((C,A)\) with state vector \(x \in \real^{m}\). For now, we assume that the system matrix can be diagonalized, such that
\begin{equation} A = W \Lambda W^{-1} \end{equation}
The columns of the matrix \(W\) are the right eigenvectors of \(A\) and \(\Lambda\) is a diagonal matrix, with the eigenvalues of \(A\) on its diagonal. For a positive natural number \(k\), there exists a well known relation between the eigenvalues and the powers of a matrix, namely \(A^k= W\Lambda^k W^{-1}\). The output of a one-dimensional state space model is equal to
\begin{equation}\label{eqn:oesc.c.pyp} y[k] = C A^k x[0] = C(W\Lambda^k W^{-1})x[0]. \end{equation}
With every eigenvector of the system matrix we associate a so called eigenmode. Take as an example \(x[0]\) equal to the $i$-th eigenvector of \(A\), which corresponds to the $i$-th column of \(W\). The eigenvalue associated to this eigenvector is indicated with \(\lambda_i\). Because \(x[0]\) is the $i$-th column of \(W\) we have that \(W^{-1} x[0] = e_i\), where \(e_i\) is the $i$-th column of the identity matrix. Using this relation, Equation~\eqref{eqn:oesc.c.pyp} becomes
\begin{equation} y[k] = CW\Lambda^k W^{-1} x[0] = CW\Lambda^k e_i = \lambda_i^k C x[0]. \end{equation}
We see that the solution still contains the vector \(x[0]\), multiplied by the scalar \(\lambda_i^k\). This illustrates that the eigenvectors of the system matrix correspond to fundamental solutions of the state space model, this fundamental solution is called an eigenmode.
The output of the state space model \((C,A)\) which can be diagonalized and has \(m\) eigenvalues \(\lambda_1,\dots,\lambda_m\) is equal to
\begin{equation} y[k] = \sum_{i=0}^n \alpha_i \lambda_i^k. \end{equation}
The values of \(\alpha_i\) depend on the initial state of the system and the output matrix.
Non-Diagonalizable case
The output of a one-dimensional state space model with non-simple eigenvalues, has been discussed in Chapter 5 of~\cite{Zadeh} for continuous systems. An eigenvalue is non-simple when the eigenvalue decomposition does not exist for this specific eigenvalue. In this case, it is only possible to calculate a Jordan block with the associated eigenvalue on the diagonal. This occurs when the geometric multiplicity of an eigenvalue is lower than its algebraic multiplicity~\cite{golub13}. The derivation of the output for discrete systems is based on the powers of the Jordan canonical form of the system matrix.
Consider the linear autonomous state space model from Equation~\eqref{eqn:1R-SS} where the system matrix \(A \in \real^{m\times m}\) is put in the Jordan canonical form. The matrix \(A\) has \(\sigma\leq m\) distinct eigenvalues, denoted by \(\lambda_1,\dots,\lambda_\sigma\). Let \(m_p\) be the algebraic multiplicity of the eigenvalue \(\lambda_p\). In~\cite{Zadeh} the subspace \(\mathcal{M}_p^l\) of the complex vector space \(\complex^{m}\) is defined as
\begin{equation} \mathcal{M}_p^l = \left\lbrace x \in \complex^{m} | (A-\lambda_p\eye)^lx =0 \right\rbrace, \end{equation}
and it is demonstrated that
\begin{equation} \mathcal{M}_p^1 \subset \mathcal{M}_p^2 \subset \dots \subset \mathcal{M}_p^{m_p} = \mathcal{M}_p^{m_p+i} \hspace{5mm} \forall i = 1,2,\dots \end{equation}
If \(x_n[0] \in \mathcal{M}_p^{n}\), but \(x_n[0] \notin \mathcal{M}_p^{n-1}\), then we will prove that
\begin{equation}\label{eqn:modes1d} x_{n}[k] = \sum_{j=1}^{n} \binom{k}{n-j}\lambda^{k-n+j}(A-\lambda\eye)^{n-j} x_n[0]. \end{equation}
This formula follows directly from the powers of a Jordan block. The large brackets in this formula represents a binomial coefficient.
Define \(J_n(\lambda)\) as the Jordan block of size \(n \times n\) with a single eigenvalue \(\lambda\). As shown in~\cite{golub13} The $k$-th power of this matrix is
\begin{equation} J_n(\lambda)^k = \begin{bmatrix} \lambda^k & \binom{k}{1}\lambda^{k-1} & \binom{k}{2}\lambda^{k-2} & \cdots & \cdots & \binom{k}{n-1}\lambda^{k-n+1} \\ & \lambda^k & \binom{k}{1}\lambda^{k-1} & \cdots & \cdots & \binom{k}{n-2}\lambda^{k-n+2} \\ & & \ddots & \ddots & \vdots & \vdots \\ & & & \ddots & \ddots & \vdots \\ & & & & \lambda^k & \binom{k}{1}\lambda^{k-1} \\ & & & & & \lambda^k \end{bmatrix}. \end{equation}
The generalized eigenvectors of this matrix, denoted by \(\lbrace e_1,\dots,e_n\rbrace\), are the columns of the identity matrix, such that
\begin{equation} e_i = [0 \cdots 1 \cdots 0]^T, \end{equation}
where the \(1\) is located at the $i$-th position. Multiplying the matrix \(J_n(\lambda)^k\) by the vector \(e_i\) selects the $i$-th column of this matrix
\begin{multline} J_n(\lambda)^k e_i = \left[ \begin{matrix} \binom{k}{i-1}\lambda^{k-i+1} & \binom{k}{i-2}\lambda^{k-i+2} & \cdots \end{matrix} \right. \\left. \begin{matrix} \binom{k}{1}\lambda^{k-1} & \lambda^k & 0 & \cdots & 0 \end{matrix} \right]^T. \end{multline}
This vector can be expressed in the eigenbasis of the Jordan block as
\begin{equation} J_n(\lambda)^k e_i = \sum_{j=1}^{i} \binom{k}{i-j}\lambda^{k-i+j} e_j. \end{equation}
Moreover, we have that \((J_n(\lambda)-\lambda\eye)e_i = e_{i-1}\), combining both expressions gives
\begin{equation}\label{eqn:ollolololol48485l0834g556} J_n(\lambda)^k e_i = \sum_{j=1}^{i} \binom{k}{i-j}\lambda^{k-i+j}(J_n(\lambda)-\lambda\eye)^{i-j} e_i. \end{equation}
From this expression we can proof Equation~\eqref{eqn:modes1d} by introducing the initial state \(x[0] \in \mathcal{M}_p^{m}\). This vector can be written as a linear combination of generalized eigenvectors \(e_1,\dots,e_r\), which form a basis of \(\mathcal{M}_p^{m}\) and \(r\) is the dimension of this space. Because equation Equation~\eqref{eqn:ollolololol48485l0834g556} is true for every vector in the basis, it is also true for all vectors span by the basis, such that
\begin{equation} x[k] = J_n(\lambda)^k x[0] = \sum_{j=1}^{m} \binom{k}{m-j}\lambda^{k-m+j}(J_n(\lambda)-\lambda\eye)^{m-j} x[0]. \end{equation}
This proves the expression of the eigenmodes of a one-dimensional state space model, as presented in Equation~\eqref{eqn:modes1d}. The output \(y[k]\) of the state space model from Equation~\eqref{eqn:1R-SS} is then equal to \(y[k] = C x[k]\).
Conclusion
In this chapter we described linear one-dimension autonomous state space models. Linear state space models can be related to polynomial equations via the theorem of Cayley–Hamilton and the characteristic polynomial. The roots of the characteristic polynomial are the eigenvalues of the associated system matrix.
The second part of this chapter discussed the observability and controllability properties of regular state space models. Two theorems for checking the observability were presented. Finally the modal decomposition of one-dimensional regular systems was derived.
All of the presented results will be extended to the class of multi-dimensional regular state space models in the later chapters.