Lets step up the game and add an extra dimension to this work, literally. From now on, we abandon plain one-dimensional systems and explore there multi-dimensional counter parts.
A multi-dimensional system is a system with evolves in multiple dimension and the system quantities, like the output and internal state, are index by multiple indices. These indices can for example be space and time.
In this chapter all classical ideas, presented in Chapter~\ref{ch:1DR} are generalized for two-dimensional state space models. This extensive system description will form the basis for the later presented realization algorithm.
The commuting state space model
Consider the two-dimensional discrete linear state space model
\begin{equation}\label{eqn:ss2d} \begin{aligned} x[k+1,l] = & Ax[k,l] \\ x[k,l+1] = & Bx[k,l] \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
with \(y[k,l] \in \real^q\) and \(x[k,l] \in \real^m\), respectively the output and the state vector of the system. The system is described by two system matrices, \(A \in \real^{m\times m}\) and \(B \in \real^{m\times m}\) and an output matrix \(C \in \real^{q\times m}\). All multivariate time series of the system, i.e.~the output and internal state, are defined on a rectangular grid, indexed by the multi-index \([k,l]\). This is illustrated in Figure~\ref{fig:grid-data}. The two dimensions of the system can represent physical quantities, like time or space.

Figure 1: Two-dimensional time series data can be represented by equidistant nodes on a rectangular grid. Every gray dot in this figure represents a single data point. Moving down on the grid has the effect of increasing the index (k) by 1, which is achieved by applying the first model equation to the state vector. Moving to the right increases the index (l) by 1. This is achieved by applying the second dynamic equation to the state vector. The arrows connecting the four data points denote two possible trajectories to go from the top left point to the bottom right while using the system equations. It is important that the presented model gives a consistent value for the state and output at every point on the grid, regardless of the path followed on that grid, i.e.~regardless of the order of operations performed on the state. In physics this property is called path-independence~cite{marsden2003vector}.
The proposed model in Equation~\eqref{eqn:ss2d} is an extension of the one-dimensional state space model. Starting from a state space model in one variable, we have extended the state vector to depend on two indices and added an extra state update equation. In order for the model to be well-posed, the state vector \(x[k,l]\) must be uniquely defined for every multi-index \([k,l]\) on the square domain of the state space model. Take for example the state vector \(x[k+1,l+1]\), when starting from \(x[k,l]\), this state can be reached in two possible ways. Visually this is demonstrated in Figure~\ref{fig:grid-data}. The round arrows in this figure show two different trajectories to go from the state vector \(x[k,l]\) to \(x[k+1,l+1]\). By using both system equations we get two expressions for the state vector at multi-index \([k+1,l+1]\), we have
\begin{equation}\label{eqn:commuting_matrices} \begin{aligned} x[k+1,l+1] & = A(x[k,l+1]) = ABx[k,l] \\ & = B(x[k+1,l]) = BA x[k,l]. \end{aligned} \end{equation}
This equation must be valid for all values of \(x[k,l]\), which can only be the case when \(AB=BA\), so \(A\) and must \(B\) commute.
The straightforward extension of the commuting state space model to higher dimensions is
\begin{equation} \begin{aligned}\label{eqn:ssnd} x[k_1+1,\dots, k_n] & = A_{1} x[k_1,\dots,k_n] \\ & \vdots \\ x[k_1,\dots, k_n+1] & = A_{n} x[k_1,\dots,k_n] \\ y[k_1,\dots,k_n] & = C x[k_1,\dots,k_n]. \end{aligned} \end{equation}
The set of \(n\) system matrices, with every matrix \(A_i\) an element of \(\real^{m\times m}\), must pairwise commute, which can be demonstrated in a similar way as for the two-dimensional model.
The model class presented in Equations~\eqref{eqn:ss2d} and~\eqref{eqn:ssnd} is called the class of commuting state space models. This model class and the identification of these models form the basis of this thesis. In this thesis we try to avoid having to write down these model equations over and over by introducing a short hand notation. In this notation we refer to the commuting state space model by only listing the model matrices. Per convention, the output matrix is denoted by \(C\) and the system matrices by \(A\) and \(B\), in two dimensions and by \(A_i\) when dealing with more dimensions. For example the two-dimensional model from Equation~\eqref{eqn:ss2d} is abbreviated as \((C,A,B)\) and \((C,A,B,x)\) if the initial state is important in the discussion, which is the case when describing controllability of this model class.
It is also important to make a clear distinction between the order and the dimension of a commuting state space model. In one-dimensional system theory, both terms are often used to represent the number of elements of the state vector. In this thesis, the dimension of the state space model indicates the number of independent multi-indices that are used to describe the `location’ of the state vector, whereas the order of the system is used to indicate the number of elements of the state vector. As an example, the system in Equation~\eqref{eqn:ssnd} has dimension \(n\) and order \(m\), we can refer to this system by writing the shorthand notation \((C,A_1,\dots,A_n)\) where \(A_i\in \real^{m\times m}\) and \(C\in \real^{q \times m}\).
State sequence
By recursively using Equation~\eqref{eqn:commuting_matrices} we find an expression for the state vector and the output at multi-index \([k,l]\) as a function of the system matrices and the initial state
\begin{equation}\label{eqn:output_2d} \begin{aligned} x[k,l] = & A^{k}B^{l}x[0,0] \\ y[k,l] = & CA^{k}B^{l}x[0,0]. \end{aligned} \end{equation}
Similarly, the expression of the output and the state vector of the system in Equation~\eqref{eqn:ssnd} as a function of the system matrices and initial state is
\begin{equation} \begin{aligned} x[k_1,\dots,k_n] & = A_1^{k_1}\dots A_n^{k_n}x[0,\dots,0] \\ y[k_1,\dots,k_n] & = C A_1^{k_1}\dots A_n^{k_n}x[0,\dots,0]. \end{aligned} \end{equation}
Example system: Modeling a chess board
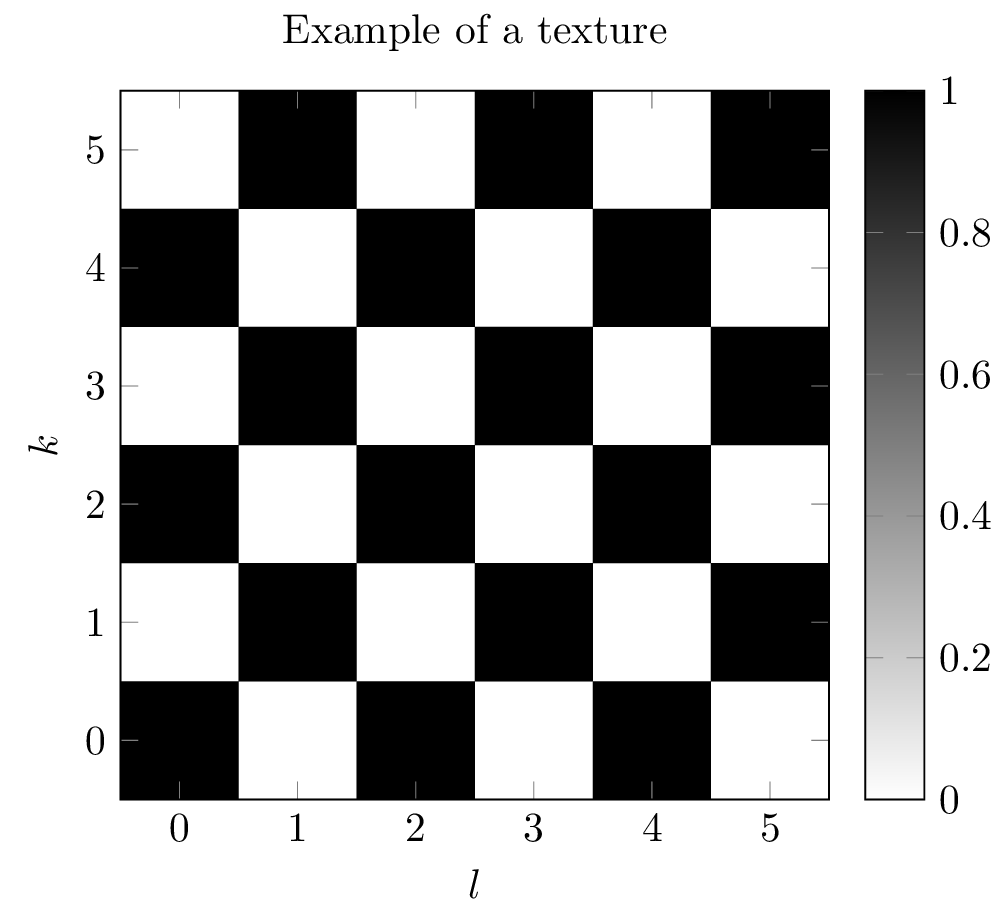
Figure 2: An image of a checkerboard pattern. This is an example texture of a two-dimensional autonomous state space model.
To give some insight in the class of commuting state space models we start with a small example system. Take the two-dimensional commuting state space model \((C,A,B)\) where
\begin{equation} A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}, B = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}, C = \begin{bmatrix}1 & 0 \end{bmatrix},x[0,0] = \begin{bmatrix}1 \\ 0 \end{bmatrix} \end{equation}
This is a system with both dimension and order 2. The output of the system is equal to
\begin{equation}\label{eqn:state_chess} y[k,l] = CA^kB^lx[0,0] = \begin{bmatrix}1 & 0\end{bmatrix}\begin{bmatrix}0 & 1 \\ 1 & 0 \end{bmatrix}^{k+l}\begin{bmatrix}1 \\ 0\end{bmatrix}. \end{equation}
When \(k+l\) is even, the output of the system is 1, when \(k+l\) is odd, the output is zero. This can be written as
\begin{equation}\label{eqn:modal_chess} y[k,l]= \frac{1}{2}(1+(-1)^{k+l}). \end{equation}
Loosely speaking, the output of this model has the shape of a checkerboard, where black and white, or zero and one, occur alternating on a regular grid, this pattern is shown in Figure~\ref{fig:checkerboard}. These patterns are sometimes called textures~\cite{dynamic_textures}.
The two expression for the output in Equations~\eqref{eqn:state_chess} and~\eqref{eqn:modal_chess} have two different forms. Equation~\eqref{eqn:state_chess} expresses the output of the system as a function of the system matrices, whereas Equation~\eqref{eqn:modal_chess} calculates the output as a function of the eigenvalues of the system matrices. The later solution is called the modal solution of the system and is discussed in Section~\ref{sec:2R-modal}.
Generalized theorem of Cayley–Hamilton
Before we introduce the concept of observability and difference equations, we introduce the theorem of Cayley–Hamilton~\cite{cayley1857memoir}. When describing observability, the theorem of Cayley–Hamilton gives an upper bound on the number of block-rows that need to be considered in the observability matrix. The theorem of Cayley–Hamilton can also be used to derive a set of difference equations associated to a given commuting state space model.
Cayley–Hamilton theorem for non-commuting matrices
In~\cite{mertzios1986generalized} a version of the theorem of Cayley–Hamilton is presented for the product of two square matrices. This theorem is stated below.
The summation of \({\binom{m}{i}}\) ordering of products of two \(m\times m\) square matrices, where in each product the first matrix appears \(i\) times and the second \(m - i\) times, is a linear combination of all possible summations of ordering of all products such that the times that both matrices appear in each product is less than \(i, m - i\), respectively.
To get a better understanding of this theorem, we first provide a simple example with two \(3\times 3\) non-commuting matrices.
Consider two non-commuting matrices
\begin{equation} A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix}, \hspace{5mm} B = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\ \end{bmatrix}. \end{equation}
It can be easily verified that \(AB \neq BA\). Take \(i\) from Theorem~\ref{thm:ch-2d} equal to 1. The summation of \({\binom{3}{1}}\) different ordering of the product between \(B\) and \(A\), where \(A\) appears once and \(B\) appears two times is than \(AB^2 + BAB + B^2A\). Theorem~\ref{thm:ch-2d} state that this summation can be written as a linear combination of the terms \(AB, BA, B^2, B, A\) and \(\eye\). By solving a linear system we find that
\begin{equation} AB^2 + BAB + B^2A = 4AB + 3BA + 2B^2 - 6B - 2A + 2\eye. \end{equation}
This solution can be checked numerically.
As a second example, consider the pair of commuting matrices
\begin{equation} A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}, \hspace{5mm} B = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}. \end{equation}
We can again verify the commutativity via an explicit calculation. Similar as in the previous example, take \(i\) from Theorem~\ref{thm:ch-2d} equal to 1. Because both matrices commute, the summation of the \({\binom{3}{1}}\) terms is now simplified as \(AB^2 + BAB + B^2A = 3 AB^2\). By solving a linear problem, we find the following polynomial equation
\begin{equation} A^2B = \frac{1}{15} \left( 18 BA + B^2 - 5 B + 12 A -11 \eye \right). \end{equation}
This expression can be verified numerically.
This second example demonstrates that Theorem~\ref{thm:ch-2d} can be simplified for the case where both matrices commute. This relaxed version is shown in the next section.
Cayley–Hamilton theorem for commuting matrices
The product of two \(m\times m\) square matrices, where the first matrix appears \(i\) times and the second \(m - i\) times, is a linear combination of all matrix products such that the times that both matrices appear in each product is less than \(i\) and \(m - i\), respectively.
This theorem can be extended to include a set of \(N\) commuting matrices.
Take the set of \(N\) pairwise commuting matrices \(A_{1},\dots,A_{N}\) of size \(m\times m\), such that
\begin{equation} A_i A_j = A_j A_i, \hspace{5mm} \forall i,j<N \end{equation}
The matrix product
\begin{equation} A_{1}^{k_{1}}A_{2}^{k_{2}}\cdots A_{N}^{k_{N}} \end{equation}
with \(k_{1} + k_{2} + \cdots + k_{N} = m\) can be written as a linear combination of matrix multiplication where in each term the matrix \(A_{i}\) appears at most \(k_{i}\) times.
The proof of this theorem follows the same structure as the proof of Theorem~\ref{thm:ch-2d} presented in~\cite{mertzios1986generalized} as we are only proving the relaxed version. In this thesis we formulate the proof for the specific case of commuting matrices formulated in~\cite{mertzios1986generalized} and add some extra explanations in every step. We also extend the results from two commuting matrices to an arbitrary set of pairwise commuting matrices. In my opinion, it is important to include this proof because it is constructive and thereby provides an algorithm to calculate the characteristic polynomials of sets of commuting matrices.
Take the collection of \(N\) commuting matrices \(A_{k}\) with \(k =1,\dots,N\) of dimension \(m\times m\). A polynomial matrix \(\hat{A}\) of first order in \(N\) complex commuting variables \((s_{1},\dots, s_{N})\) is defined as
\begin{equation}\label{eqn:Ahat} \hat{A}(s_{1},\dots,s_{N}) = \sum_{k=1}^{N} A_{k}s_{k}. \end{equation}
The characteristic equation of this matrix is defined as \(\Delta(z) = \det(z\eye - \hat{A}(s_{1},\dots,s_{N}) )\) which can be written as
\begin{equation}\label{eqn:char_poly} \Delta(z) = z^{m} + q_{m-1}z^{m-1}+ \dots +q_{1}z + q_{0}. \end{equation}
This is a polynomial expression in \(z\) of order \(m\). The coefficients of this polynomial \((q_{m-1},\dots,q_{0})\) are by itself functions of the variables \((s_{1},\dots, s_{N})\). By applying Faddeev–LeVerrier algorithm~\cite{gantmacher1960theory} it is easy to see that the factors \(q_{k}\) are polynomial expressions in \((s_{1},\dots,s_{N})\) with a total degree equal to or less than \(m-k\) this follows directly from the recursion steps in Faddeev–LeVerrier algorithm and the fact that \(\hat{A}\) is a linear function of the variables $si$~\cite{Mertzios1984}.
The total degree of a monomial is the sum of all powers of the individual variables. For example, the monomial \(s_{1}^{2}s_{2}s_{3}\) has a total degree of \(2+1+1=4\). The total degree of a polynomial is the heights total degree of its monomials.
Following the classical theorem of Cayley–Hamilton, the matrix \(\hat{A}\) solves its own characteristic equation represented by Equation~\eqref{eqn:char_poly}
\begin{equation}\label{eqn:ch} 0 = \hat{A}^{m} + q_{m-1}\hat{A}^{m-1}+ \dots +q_{1}\hat{A} + q_{0}\eye. \end{equation}
The terms \(\hat{A}^{k}\) are polynomial matrices in \((s_{1},\dots,s_{N})\) with a total degree less than or equal to \(k\) and thus the total degree of every factor \(q_{k}\hat{A}^{k}\) is at most \(m\) in the variables \((s_{1},\dots,s_{N})\). The expression \(\hat{A}^{k}\) from Equation~\eqref{eqn:Ahat}, can also be regarded as a polynomial in the different matrices \(A_{1},\dots,A_{N}\), the total degree of this polynomial is than also at most \(k\). It is important for all the matrices to commute, if this would not be the case the polynomial expression \(\hat{A}^{k}\) must include all possible arrangements of taking \(k\) matrices from a collection of the \(N\) matrices \(A_{1},\dots,A_{N}\). For example, when we take \(N=2\) and \(k=2\), we have
\begin{equation} (s_{1}A_{1}+s_{2}A_{2})^{2} = s_{1}^{2}A_{1}^{2}+s_{1}s_{2}A_{1}A_{2} + s_{2}s_{1}A_{2}A_{1}+s_{2}^{2}A_{2}^{2}. \end{equation}
If \(A_{1}\) and \(A_{2}\) commute, this expression can be simplified to \(s_{1}^{2}A_{1}^{2}+2s_{1}s_{2}A_{1}A_{2}+s_{2}^{2}A_{2}^{2}\).
Because the total degree as the polynomial in the variables \((s_{1},\dots, s_{N})\) of Equation~\eqref{eqn:ch} is bound by \(m\), the terms in the sum can be reordered in the following way
\begin{equation*} \hat{A}^{m} + \dots + q_{0}\eye = \sum_{n_{i} = 0}^{m}\sum_{\tiny\begin{matrix} k_{1}+k_{2}+\\ \cdots +k_{N}=n_{i} \end{matrix}} f_{k_{1},\dots,k_{N}}(A_{1},\dots,A_{N})\prod_{t=1}^{N}(s_{t})^{k_{t}}. \end{equation*}
The first sum is the sum over all total degrees up to and including \(m\), the second sum is the sum over all possible combinations of powers with a total degree equal to \(n_{i}\) and the last product forms the different monomials with the corresponding degree \(n_{i}\).
This is a polynomial expression in \(s_{1},\dots,s_{N}\) that must be identically equal to \(0\) as a result of Cayley–Hamilton. A polynomial is only identically zero if all coefficient of the polynomial are zero, for this reason we have
\begin{equation*} f_{k_{1},\dots,k_{N}}(A_{1},\dots,A_{N}) = 0 \hspace{.5cm} \forall 0\leq k_{1}+\dots + k_{N} \leq m. \end{equation*}
The polynomial \(f_{k_{1},\dots,k_{N}}(A_{1},\dots,A_{N})\) with \(k_{1}+\dots+k_{N} = m\) has a unique monomial in the matrices \(A_{i}\) of degree \((k_{1},\dots,k_{N})\), this is the term that appears in the expression of \(\hat{A}^{m}\) because the other matrix exponents yield a lower total degree in the matrix monomials. Because of this uniqueness of the term with total degree \(m\) the factors \(f_{k_{1},\dots,k_{N}}\) can be rewritten as
\begin{equation} A_{1}^{k_{1}}\dots A_{N}^{k_{N}} = \sum_{n_{i} = 1}^{m-1}\sum _{\tiny\begin{matrix} l_{1}+l_{2}+\\ \cdots +l_{N}=n_{i} \end{matrix}} a_{l_{1},\dots,l_{N}}A_{1}^{l_{1}}\dots A_{N}^{l_{N}}. \end{equation}
This proves the theorem.
The proof of the extended theorem of Cayley–Hamilton is a constructive proof which allows for a direct calculation of the linear relations between \(m\) commuting matrices. To illustrate this proof, an example is provide.
Example: Cayley–Hamilton for 2 commuting matrices
In the previous section, two examples of the theorem of Cayley–Hamilton for commuting and non-commuting matrices were provide. In these previous examples, the coefficients of the linear combination were obtained by solving a linear problem. The proof presented above, is a constructive proof and the results can be directly used to find the relation between the matrix powers. This is shown in the next example for a pair of commuting matrices of size \(2 \times 2\), the matrices are
\begin{equation} \begin{matrix} A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, & B = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}. \end{matrix} \end{equation}
Take two independent variables \(s_1\) and \(s_2\) and define the matrix \(\hat{A}\) as described in the proof of Theorem~\ref{thm:thm_CH}
\begin{equation} \hat{A} = A s_{1} + B s_{2} = \begin{bmatrix} s_{1} + s_{2} & s_{1} + 2s_{2} \\ 0 & s_{1} + s_{2} \\ \end{bmatrix}. \end{equation}
Next, we calculate the characteristic polynomial of this matrix, which is equal to
\begin{equation}\label{eqn:characteristic_example} \Delta(z) = \det(z\eye-\hat{A}) = (z-(s_{1}+s_{2}))^{2} = z^{2}-2z(s_1+s_2)+(s_{1}+s_{2})^{2}. \end{equation}
According to the theorem of Cayley–Hamilton the matrix \(\hat{A}\) satisfies this equation. Substituting \(\hat{A}\) in Equation~\eqref{eqn:characteristic_example} leads to
\begin{equation} (A s_{1} + B s_{2})^{2} -2(s_{1}+s_{2})(A s_{1} + B s_{2}) + (s_{1}+s_{2})^{2} = 0. \end{equation}
Note that this expression is the same as Equation~\eqref{eqn:ch}. Rearranging the different components of this polynomial leads to
\begin{equation} \begin{matrix} (A^{2}-2A + \eye)s_{1}^{2} + (B^{2}-2B + \eye)s_{2}^{2} \\ + (2AB -2A -2B+2\eye)s_1s_2 = 0. \end{matrix} \end{equation}
The three expression corresponding to the three monomials \((s_{1}^{2}, s_{2}^{2},s_{1}s_{2})\) are identically equal to zero
\begin{equation} \begin{matrix} A^{2}-2A + \eye = 0 \\ B^{2}-2B + \eye = 0 \\ AB -A -B+\eye = 0. \end{matrix} \end{equation}
The first two expressions only depend on a single matrix respectively \(A\) and \(B\). The third expression depends on both matrices \(A\) and \(B\). We can validate this result numerically by plugging in the known values of \(A\) and \(B\). For the third expression we get as an example
\renewcommand{\Aone}{\begin{bmatrix}1 & 1 \\0 & 1 \end{bmatrix}} \renewcommand{\Atwo}{\begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}}
\begin{equation} \Aone\Atwo -\Aone -\Atwo+\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} = \begin{bmatrix}1 & 3 \\ 0 & 1\end{bmatrix} - \begin{bmatrix}1 & 3 \\ 0 & 1\end{bmatrix} = 0. \end{equation}
The other two equations can be checked in a similar manner.
Difference equation
A linear two-dimensional autonomous discrete system can be represented by the following difference equation
\begin{equation}\label{eqn:nDsystemDiscrete} \sum_{i=0}^{n_{1}} \sum_{j=0}^{n_{2}} \alpha_{i,j}y[k_{1}+i,k_{2}+j] = 0. \end{equation}
The values \(k_{1}\) and \(k_{2}\) are two discrete shift variables. The order of the difference equation is defined as the tuple \((n_{1},n_{2})\). This assumes of course that there is at least one parameter \(\alpha_{n_1,j}\) and \(\alpha_{i,n_2}\) not equal to zero, otherwise we can reduce the summation indices in Equation~\eqref{eqn:nDsystemDiscrete}.
We can calculate the difference equation associated to a commuting state space model by using the results from Sections~\ref{sec:2R-CH}. Consider the commuting state space model \((C,A,B)\) of order \(m\). According to the generalized theorem of Cayley–Hamilton, there exits a polynomial \(f(s_1,s_2)\) of total degree \(m\) such that \(f(A,B) = 0\). This polynomial can in general be written as
\begin{equation} f(s_1,s_2) = \sum_{i=0,j=0}^{i+j\leq m} \alpha_{i,j} s_1^i s_2^j. \end{equation}
After substituting \(A\) for \(s_1\) and \(B\) for \(s_2\) and pre and post multiplying the previous equation respectively by the output matrix \(C\) and a state vector \(x\), we get
\begin{equation} \sum_{i=0,j=0}^{i+j\leq m} \alpha_{i,j} CA_1^i A_2^jx = 0. \end{equation}
This shows that the generalized theorem of Cayley–Hamilton can be used to derive a difference equation for a commuting state space model. We can also conclude that the solution of a commuting state space model satisfies multiple difference equations. This is because we can derive multiple polynomial equations from the theorem of Cayley–Hamilton. Two trivial cases are given by
\begin{equation} f_1(s_1,s_2) = f_{A_1}(s_1)~\text{and}~f_2(s_1,s_2) = f_{A_2}(s_2), \end{equation}
where \(f_{A_1}\) and \(f_{A_2}\) are respectively the characteristic polynomial for the matrices \(A_1\) and \(A_2\).
Observability
The concept of observability of multi-dimensional systems has been discussed many times in the past. For example in the behavioral framework by Willems~\cite{willems1997introduction}. Willems states that the internal state of a state space model is observable if and only if it can be uniquely determined when the output and the system dynamics are known. In his framework, the internal state and the output together form the trajectory of the system.
We start this section by defining the concept of observability for 2D commuting state space models.
A commuting state space model is observable if and only if the entire state sequence can be estimated based on a finite set of measurements and when the system matrices are known.
We formulate two criteria to check the observability of the class of commuting state space models.
The observability matrix
By applying the idea of Willems and Kalman, we can formulate the condition of observability for the class of two-dimensional commuting state space models described in Equation~\eqref{eqn:ss2d}. Given the output measurements \(y[k,l]\) of a discrete commuting state state space model, for some values of the discrete multi-index \([k,l]\). \textit{When is it possible to retrieve the state vector $x[k,l]$ based on the observed output values?}
To answer this question we introduce the observability matrix \(\obs\) for a two-dimensional commuting state space model~\cite{dreesen2013back}, with output matrix \(C \in \real^{q\times m}\) and commuting system matrices \(A\in \real^{m\times m}\) and \(B\in \real^{m\times m}\)
\begin{equation}\label{eqn:obsmat2d} \obs = \begin{bmatrix} C \\ \hline CA \\ CB \\ \hline CA^2 \\ CA B \\ C B^{2} \\ \hline \vdots \\ \hline C A^{m-1} \\ \vdots \\ C B^{m-1} \end{bmatrix}. \end{equation}
The lines in this matrix indicate that the observability matrix is structured in \(m\) block matrices. Every one of these blocks in characterized by a specific order. The order of a block indicates the total number of times the matrices \(A\) and \(B\) appear in the multiplication in each row of the block. As an example, all block rows \(CA^kB^l\) of the block with order \(q\) satisfies the relation where \(k+l=q\).
Consider the state vector \(x[0,0]\). From the output equation of the commuting state space model it follows that
\begin{equation} \obs x[0,0] = \begin{bmatrix} Cx[0,0] \\ \hline CAx[0,0] \\ CBx[0,0] \\ \hline CA^2x[0,0] \\ CABx[0,0] \\ CB^{2}x[0,0] \\ \hline \vdots \\ \hline CA^{m-1}x[0,0] \\ \vdots \\ CB^{m-1} x[0,0] \end{bmatrix} = \mathcal{Y} = \begin{bmatrix} y[0,0] \\ \hline y[1,0] \\ y[0,1] \\ \hline y[2,0] \\ y[1,1] \\ y[0,2] \\ \hline \vdots \\ \hline y[m-1,0] \\ \vdots \\ y[0,m-1] \end{bmatrix}. \end{equation}
Only if the matrix \(\obs\) is of full column rank, the state vector \(x[0,0]\) can be uniquely determined when the output \(\mathcal{Y}\) is known, and the pseudo-inverse, indicated with \(\dagger\) of \(\obs\) exists. The initial state is retrieved via
\begin{equation} x[0,0] = \obs^{\dagger}\mathcal{Y} = (\obs^{T}\obs)^{-1}\obs^{T}\mathcal{Y}. \end{equation}
Starting from this state, the entire state sequence can be estimated. This result implies that, when the system matrices and the output matrix are known, it is possible to reconstruct the initial state, and by extension the entire state sequence, based on the finite set of observations present in the matrix \(\mathcal{Y}\). This is exactly Kalman’s definition of observability as stated in Definition~\ref{defn:2R-obs}.
From the extended theorem of Cayley–Hamilton, formulated in Theorem~\ref{thm:ch-2d}, it follows that adding extra blocks of higher order won’t affect the rank of the observability matrix because they are linearly depending on the blocks of lower order. It is thereby sufficient to construct the observability matrix up to and including the block of order \(m-1\). The results above are summarized in the following theorem.
The state space model of Equation~\eqref{eqn:ss2d} of order \(m\), is observable if and only if the two-dimensional observability matrix from Equation~\eqref{eqn:obsmat2d} has rank \(m\). % Under this condition, the initial state, and by extension the complete state sequence, can be uniquely reconstructed from a finite set of observed output data.
Popov–-Belevitch–-Hautus
An equivalent condition to guarantee the observability of a two-dimensional system can be formulated by extending the Popov–Belevitch–Hautus-test for two-dimensional systems.
The state space model from Equation~\eqref{eqn:ss2d} of order \(m\) with \(q\) outputs, is observable if and only if the \((2m+q)\times m\) dimensional matrix
\begin{equation}\label{eqn:hautus2d} \begin{bmatrix} A - \lambda_1 \eye \\ B - \lambda_2 \eye \\ C \end{bmatrix}, \end{equation}
has rank \(m\) for all possibly complex pairs of \((\lambda_1,\lambda_2)\).
Proof equivalency of both criteria
We prove the equivalence between the two criteria formulated in Theorem~\ref{thm:obs2d} and~\ref{thm:2R-PBH-obs}.
Suppose the matrix in Equation~\eqref{eqn:hautus2d} is rank deficient for some value of \((\lambda_1,\lambda_2)\). This implies that there exists a non-trivial vector \(v\) in the right null space of this matrix. The vector in the null space satisfies the following equations
\begin{equation} \begin{matrix} Av = \lambda_1 v \\ Bv = \lambda_2 v \\ Cv = 0 \\ \end{matrix}, \end{equation}
i.e. the vector \(v\) is a common eigenvector of the matrices \(A\) and \(B\) and is orthogonal to \(C\).
For every positive real integer value \(k,l\) we now have that \(CA^kB^lv = \lambda_1^k\lambda_2^lCv = 0\) and thus
\begin{equation} \obs = \begin{bmatrix} C^T & (CA)^T & (CB)^T & \cdots & (CAB^{n-1})^T & \cdots & (CB^{n-1})^T \end{bmatrix}^{T}v = 0. \end{equation}
The observability matrix has a non-trivial right null space and is thus rank deficient. This shows that when the matrix in Equation~\eqref{eqn:hautus2d} is rank deficient, the observability matrix is also rank deficient and the system is therefore not observable.
To prove the equivalence the other way around, we assume the observability matrix to be rank deficient and demonstrate that the Hautus criteria for observability is not satisfied. When the observability matrix is rank deficient, it implies that there exists a non-trivial vector \(v\) (i.e.~not identically equal to zero) such that
\begin{equation}\label{eqn:obs_not_full} \obs = \begin{bmatrix} C^T & (CA)^T & (CB)^T & \cdots & (CAB^{n-1})^T & \cdots & (CB^{n-1})^T \end{bmatrix}^{T}v = 0. \end{equation}
Because the vector \(v\) lies in the right null space of the observability matrix, we have that \(CA^kB^l v = 0\) for all indices \(k,l\geq 0\) smaller than \(m\).
Take a polynomial \(\psi_1(z)\), not identically zero, of minimal degree such that \(\psi_1(A)v = 0\). This polynomial exist and has degree \(d\), the maximum degree is limited as a consequence of the theorem of Cayley–Hamilton, for this reason we have that \(1\leq d\leq m\). The existence can easily be verified, for every square matrix \(A\) of size $m× m$there always exists a $n-$th order (\(n\leq m\)) polynomial such that \(p(A)=0\), namely the characteristic polynomial and we have that \(p(A)v=0\). However this polynomial is not guaranteed to be the polynomial of lowest degree.
The degree of \(\psi_1(z)\) is also always larger than 0. If the degree was 0, the expression \(\psi_1(A)\) would be equal to a scalar multiplication with \(A^{0}=\eye\). If \(\psi_1(z)\) is not identically zero \(\psi_1(A)\) would be of full rank and \(\psi_1(A)v\neq 0\).
It follows that the polynomial \(\psi_1\) exists and has at least one (possibly complex) root denoted by \(\lambda_1\) and can thus be factorized as
\begin{equation} \psi_1(z) = (\lambda_1 - z) \phi_1(z). \end{equation}
Define the (possibly complex) vector \(\eta_1 = \phi_1(A)v\). Because of the assumption that \(\psi_1(z)\) is the polynomial of minimal degree such that \(\psi_1(A)v=0\) and because the degree of \(\phi_{1}(z)\) is one lower than that of \(\psi_1(z)\), we have that \(\eta_1 \neq 0\). Furthermore, \(\eta_1\) is an eigenvector of the matrix \(A\) because
\begin{equation} (\lambda_1\eye - A) \eta_1 = (\lambda_1\eye - A) \phi_1(A)v = \psi_1(A)v = 0, \end{equation}
and thus
\begin{equation} A \eta_1 = \lambda_1 \eta_1. \end{equation}
Next, define the polynomial \(\psi_2(z)\) to be the polynomial of smallest degree such that
\begin{equation} \psi_2(B) \eta_1 = 0. \end{equation}
Following the same reasoning as before, this polynomial always exists and has at least one (possibly complex) root, denoted by \(\lambda_2\). The polynomial \(\psi_2(z)\) can be factorized as
\begin{equation} \psi_2(z) = (\lambda_2 - z) \phi_2(z), \end{equation}
for some value of \(\lambda_2\).
Define the vector \(\eta_2 = \phi_2(B)\eta_1\). By construction \(\eta_2\) is not equal to zero, because the degree \(\phi_2(z)\) is one lower that the degree of \(\psi_2(z)\). The vector \(\eta_2\) is an eigenvector of \(B\) because
\begin{equation} (\lambda_2\eye - B) \eta_2 = (\lambda_2\eye - B) \phi_2(B) \eta_1 = \psi_2(B) \eta_1 = 0, \end{equation}
Furthermore, the vector \(\eta_2\) is also an eigenvector of the \(A\) because
\begin{equation} (A - \lambda_1\eye)\eta_2 = (A - \lambda_1\eye)\phi_2(B)\eta_1 = \phi_2(B)(A - \lambda_1\eye)\eta_1 = 0. \end{equation}
This last step in the equation above follows from the commutation of both matrices \(A_{1}\) and \(A_{2}\).
We still have to prove that \(C\) is orthogonal to \(\eta_{2}\).
From the definition of \(\eta_{2}\) we know that,
\begin{equation} C\eta_{2} = C\psi_1(A_{1})\psi_2(A_{2}) v = C\left(\sum_{k=0}^{m_1}a_k A_{1}^{k}\right) \left(\sum_{l=0}^{m_2}b_k A_{2}^{l}\right) v = \sum_{k=1,l=1}^{m_{1},m_{2}}a_{k}b_{l}CA_{1}^{k}A_{2}^{l}v \end{equation}
for some values \(m_{1}, m_{2}<m\) and polynomial coefficients \(a_{k}\) and \(b_{k}\) for \(\psi_{1}\) and \(\psi_{2}\) respectively.
From Equation~\eqref{eqn:obs_not_full} we know that every term in the sum \(CA_{1}^{k}A_{2}^{l}v\) is equal to zero.
Because the sum has a finite number of terms, the sum itself is also zero, this proves that \(C\eta_{2} = 0\).
Combing these results proves that
\begin{equation} \begin{bmatrix} A - \lambda_1 \eye \\ B - \lambda_2 \eye \\ C \end{bmatrix}\eta_2 = 0 \end{equation}
The vector \(\eta_2\) is a common eigenvector of both matrices \(A\) and \(B\) that is orthogonal to \(C\). Because this tall matrix has a non-trivial right null space it is rank deficient.
\begin{equation} \text{rank} \left( \begin{bmatrix} A - \lambda_1 \eye \\ B - \lambda_2 \eye \\ C \end{bmatrix} \right) < m. \end{equation}
Both statements prove the equivalence between the Popov–Belevitch–-Hautus lemma for two-dimensional systems and the observability criteria from Kalman.
Non-observable systems and column compressions
When the observability matrix of a commuting state space model is rank deficient, we say that the system is not observable. Similar as for the one-dimensional state space model, we can calculate a column compression, to reduce the commuting state space model to an observable system.
Consider the commuting state space model \((C,A,B)\) of order \(m\), which has an observability \(\obs\) matrix of rank \(r<m\). We can calculate the singular value decomposition of this matrix, as
\begin{equation} USV^T = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix} = \obs \end{equation}
By post multiplying the observability matrix with the right singular vectors, we get the matrix \(\obs_V\), such that
\begin{equation} \obs_V = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \Sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix} \begin{bmatrix} V_0 & V_1 \end{bmatrix} = \begin{bmatrix} U_0 \Sigma_0 & 0 \end{bmatrix}. \end{equation}
This is the same column compression as performed on the one-dimensional regular system. The first \(r\) columns are non-zero, followed by \(m-r\) zero-columns.
Note that the observability matrix for a two-dimensional commuting state space model contains all block rows of two observability matrices of two state space models, namely \((C,A)\) and \((C,B)\), formed by the individual system matrices. The influence of a column-compression on both matrices individually, has been studied before in Chapter~\ref{ch:1DR}. We can therefore conclude that the output matrix and both system matrices are transformed as \(CV = \begin{bmatrix} C_0 & 0\end{bmatrix}\) and
\begin{equation} V^TA V = \begin{bmatrix} A_{0,0} & 0 \\ A_{1,0} & A_{1,1} \end{bmatrix},~ V^TB V = \begin{bmatrix} B_{0,0} & 0 \\ B_{1,0} & B_{1,1} \end{bmatrix}. \end{equation}
The system \((C_0,A_{0,0},B_{0,0})\) is the observable subsystem of \((C,A,B)\).
Recursive observability matrix
In this thesis we introduce a second observability-like matrix, called the recursive observability matrix. This matrix has the structure of a block observability matrix, where all blocks are observability matrices by them selves. The recursive observability matrix \(\robs\) for a two-dimensional commuting state space model, with output matrix \(C \in \real^{q\times m}\) and commuting system matrices \(A\in \real^{m\times m}\) and \(B\in \real^{m\times m}\) is defined as
\begin{equation} \robs = \begin{bmatrix} \robs_0 \\ \robs_1 \\ \vdots \\ \robs_{m-1} \end{bmatrix}, \end{equation}
where
\begin{equation} \robs_i = \begin{bmatrix} C B^i \\ C AB^i \\ \vdots \\ C A^{m-1}B^i \\ \end{bmatrix}. \end{equation}
The size of \(\robs\) is \((qm^2) \times m\).
The recursive observability matrix and the observability matrix are related with each other. Note that the rows of the observability matrix are given by the set
\begin{equation} S_1 = \left\{ C A^k B^l | 0\leq k \wedge 0 \leq l \wedge k+l \leq m-1 \right\}. \end{equation}
On the other hand, the rows of the recursive observability matrix are given by
\begin{equation} S_2 = \left\{ C A^k B^l | 0\leq k \leq m-1 \wedge 0 \leq l \leq m-1 \right\}. \end{equation}
It is clear that \(\spann{S_1}\subseteq \spann{S_2}\). However from the theorem of Cayley–Hamilton for commuting matrices we also know that for all values of \(0\leq p\leq m\), the term \(A^{m} B^{m-p}\) is linearly dependent on the set of matrices \(\eye, A,B,A^2,\dots,AB^{m-1},B^m\), such that there exists coefficients \(\alpha_{i,j}\) for which
\begin{equation} A^{m} B^{m-p} = \sum_{i,j}^{i+j<m-1} \alpha_{i,j} A^{i}B^{j}. \end{equation}
This implies that \(\spann{S_2}\subseteq \spann{S_1}\). When combining both statements, we can conclude that \(\spann{S_2} = \spann{S_1}\). The rank of both the observability and the recursive observability will be the same. In the next chapter we will show that this is not the case when working with the class of commuting descriptor systems.
Controllability
Dual to the property of observability, we generalize the concept of controllability for two-dimensional commuting state space models. We will first introduce the generalized state sequence matrix. This matrix is based on the state sequence matrix of regular state space models and has a similar structure as the generalized observability matrix.
Definition of controllability
Controllability of two-dimensional commuting state space models is defined as follows;
A two-dimensional commuting state space model with commuting system matrices \(A\) and \(B\) of order \(m\) is controllable with initial state \(x[0,0]\) if and only if
\begin{equation} \text{span}\left( \left\{ x[k,l] = A^kB^lx[0,0] | \forall k,l> 0 \right\} \right) = \real^m. \end{equation}
Note that the controllability of a system does not depend the output matrix \(C\), but only on the initial state of the system. The definition of controllability implies that a two-dimensional commuting state space model is controllable when the entire space \(\real^m\) can be reached when starting from the initial state. To test if a system is controllable we first introduce the following lemma.
A two-dimensional commuting state space model with commuting system matrices \(A\) and \(B\) of order \(m\) is controllable with initial state \(x[0,0]\) if and only if
\begin{equation} \text{span}\left( \left\{ x[k,l] = A^kB^lx[0,0] | \forall k,l>0 \land k+l < m \right\} \right) = \real^m. \end{equation}
The only difference between this lemma and Definition~\ref{def:2R-cont} is the index-range of the state sequence. To proof this lemma we first introduce some notation. We denote the vector spaces from Definition~\ref{def:2R-cont} and Lemma~\ref{lem:2R-cont} respectively as \(V_{\infty}\) and \(V_m\).
To proof this lemma we need to proof that
\begin{equation} V_{\infty} = V_m \end{equation}
It is clear that
\begin{equation}\label{2R:subset_eq_1} V_{\infty} \supseteq V_m \end{equation}
To proof the equality we only need to proof that \(V_{\infty} \subseteq V_m\)
Take a vector \(x[k,l]\) with \(k>0\) and \(l>0\) at random, which is an element of \(V_{\infty}\) by construction. We will show that this vector also lies in \(V_{m}\). There are two options to consider, either \(k+l\) is smaller than \(m\), in which case we have that \(x[k,l] \in V_{m}\), as per construction, and the second case, where \(k+l>m\). Consider the second case. From the model equations for the commuting state space model we have that
\begin{equation} x[k,l] = A^kB^l x[0,0]. \end{equation}
According to the Theorem of Cayley–Hamilton, \(A^kB^l\) can be written as a linear combination of lower powers of both matrices \(A\) and \(B\), as such
\begin{equation} A^kB^l = \sum_{i=0,j=0}^{i+j<m} \alpha_{i,j} A^iB^j, \end{equation}
for some constant values \(\alpha_{i,j}\), which depend on both system matrices and can be calculated using Cayley–Hamilton. Multiplying this equality from the right by the vector \(x[0,0]\) gives
\begin{equation} x[k,l] = A^kB^lx[0,0] = \sum_{i=0,j=0}^{i+j<m} \alpha_{i,j} A^iB^jx[0,0] = \sum_{i=0,j=0}^{i+j<m} \alpha_{i,j} x[i,j]. \end{equation}
Which proofs that \(x[k,l]\) is a linear combination of vectors \(x[i,j]\), where \(i+j<m\). It thus follows that \(x[k,l] \in V_m\). Because \(x[k,l]\) was taken at random from \(V_{\infty}\) we have prove that
\begin{equation}\label{2R:subset_eq_2} V_{\infty} \subseteq V_m. \end{equation}
Combing Equation~\eqref{2R:subset_eq_1} and~\eqref{2R:subset_eq_2} demonstrates that
\begin{equation} V_{\infty} = V_m, \end{equation}
which proofs Lemma~\ref{lem:2R-cont}.
The state sequence matrix
The generalized state sequence matrix, for the commuting state space model \((C,A,B)\) with initial state \(x_{0,0}\) is given by
\begin{equation} \begin{bmatrix} x_{0,0} & \vert~x_{1,0} & x_{0,1} & \vert~x_{2,0} & x_{1,1} & x_{0,2} & \vert~\cdots & \vert~x_{m-1,0} & \cdots & x_{0,m-1} \end{bmatrix}. \end{equation}
Note that we use a subscript notation to indicate the position of the state instead of the more conventional indexation with square brackets, this is done with the intent to reduce the overall width of the equation. The vertical lines in the matrix denote different block matrices. Each of the block matrices has a constant sum of the indices. The first block only contains \(x_{0,0}\), which has an index sum of 0. In the second block we find two states, \(x_{0,1}\) and \(x_{1,0}\). The sum of both indices is respectively \(1+0\) and \(0+1\).
Testing controllability
We describe two tests to verify if a system is controllable or not. These two tests are similar to the results presented when describing observability.
A two-dimensional commuting state space model with commuting system matrices \(A\) and \(B\) of order \(m\) is controllable with initial state \(x[0,0]\) if and only if the state sequence matrix is of full rank.
The proof of this theorem follows directly from the result of Lemma~\ref{lem:2R-cont}. Note that the columns of the state sequence matrix are exactly the vectors which span \(V_m\) is Lemma~\ref{lem:2R-cont}. If and only if the state sequence matrix has full rank we know that the column space is equal to \(\real^m\). This is the required condition for controllability.
The PBH-test can also be formulated to check the controllability of a commuting state space model.
The state space model of Equation~\eqref{eqn:ss2d} is observable if and only if the matrix of size \(m\times(2m+1)\)
\begin{equation}\label{eqn:hautus2d-controllability} \begin{bmatrix} A_1 - \lambda_1 \eye & A_2 - \lambda_2 \eye & x[0,0] \end{bmatrix} \end{equation}
is of full rank for every value of the complex pair \((\lambda_1,\lambda_2)\).
The proof of this lemma is conceptually the same as that of Lemma~\ref{thm:2R-PBH-obs}.
Non-controllable systems and row compressions
When the commuting state space model is non-controllable we can perform a row compression on the state sequence matrix. This compression follows the same calculations as shown in Section~\ref{sec:2R-colcomp}.
The recursive state sequence matrix
In a similar way as for observability, we can introduce the recursive state sequence matrix. This matrix will have the same rank as the state sequence matrix but it has more columns. The matrix is defined as; The recursive state sequence matrix \(\rX\) for a two-dimensional commuting state space model, with output matrix \(C \in \real^{q\times m}\) and commuting system matrices \(A\in \real^{m\times m}\) and \(B\in \real^{m\times m}\) and initial state \(x\) is defined as
\begin{equation} \chi = \begin{bmatrix} \rX_0 & \rX_1 & \cdots & \rX_{m-1} \end{bmatrix}, \end{equation}
where
\begin{equation} \rX_i = \begin{bmatrix} B^ix & AB^ix & \cdots & A^{m-1}B^i x \end{bmatrix}. \end{equation}
The size of \(\rX\) is \((qm^2) \times m\).
Extended observability and state sequence matrices
Similar as for one-dimensional systems, we can introduce the extended observability and extended state sequence matrices, as well as the extended recursive observability and extended recursive state sequence matrices. The extended observability and state sequence matrices are characterized by an order, which determines respectively the number of block rows and block columns of these matrices.
The extended observability matrix of order \(n\) denoted as \(\obs_{0|n-1}\) is defined as the observability matrix with a total of \(n\) blocks. The observability matrix is thus equal to the extended observability matrix of the same order as the underlying state space model. In a similar way, we define the extended state sequence matrix \(\X_{0|n-1}\) of order \(n\) as the state sequences matrix with \(n\) block columns. When the order of the matrix is the same as the order of the underlying state space model, the extended state sequence matrix becomes the same as the state sequence matrix.
For the recursive counterparts of the observability and state sequence matrices, two orders need to be determined, one determining the block sizes and one determining the number of blocks. The extended recursive observability matrix (\gls{EROM}) of order \((\mu,\nu)\) is denoted by \(\robs_{0|\mu-1,0|\nu-1}\). This matrix consists of \(\nu\) blocks with each block having \(q\mu\) rows, where \(q\) denotes the number of outputs of the system. For a commuting state space model of order \(m\), the extended recursive observability matrix of order \(\robs_{0|m-1,0|m-1}\) is the same as the recursive observability matrix. The extended recursive state sequence matrix (\gls{ERSM}) of order \((\mu,\nu)\), denoted as \(\rX_{0|\mu-1,0|\nu-1}\) is defined in the same way as the extended recursive observability matrix. The matrix \(\rX_{0|\mu-1,0|\nu-1}\) consists of \(\nu\) block columns, with each block having \(\nu\) columns. Again, \(\rX_{0|m-1,0|m-1}\) is the recursive state sequence matrix of the commuting state space model with order \(m\).
Kalman decomposition
The notion of controllability, observability and column/row compressions has been extended to two-dimensional commuting states space models in this chapter. The combination of these concepts result in the introduction of the Kalman decomposition for commuting state space models.
For a given commuting state space model \((C,A,B)\) with initial state \(x_{0,0}\in \real^m\), the Kalman decomposition is defined as the system \((\hat{C},\hat{A},\hat{B})\) with initial state \(\hat{x}_{0,0}\) as
\begin{equation} \begin{aligned} \hat{C} & = C T^{-1}, \\ \hat{A} & = T A T^{-1}, \\ \hat{B} & = T B T^{-1}, \\ \hat{x}_{0,0} & = T x_{0,0}. \\ \end{aligned} \end{equation}
The matrix \(T^{-1}\) is an invertible matrix of size \(m\times m\) defined as
\begin{eqnarray}\label{eqn:2R_kalman} T^{-1}= \begin{bmatrix} T_{co} & T_{\overline{c}o} & T_{c\overline{o}} & T_{\overline{co}} \end{bmatrix}. \end{eqnarray}
The four submatrices are
- The columns of \(T_{co}\) form a basis for the controllable and reachable part of the system.
- The columns \(T_{\overline{c}o}\) form a basis for the observable but non-controllable part of the system.
- The columns \(T_{c\overline{o}}\) form a basis for the controllable but non-observable part of the system.
- The columns \(T_{\overline{co}}\) form a basis for the part of the system that is neither controllable nor observable.
In this basis, the system matrices can be written as
\begin{equation}\label{eqn:2R-kalman-dec1} \hat{A} = \begin{bmatrix} A_{co} & A_{12} & A_{13} & A_{14} \\ 0 & A_{co} & 0 & A_{24} \\ 0 & 0 & A_{\overline{co}} & A_{34} \\ 0 & 0 & 0 & A_{\overline{c}o} \end{bmatrix}, \hat{B} = \begin{bmatrix} B_{co} & B_{12} & B_{13} & B_{14} \\ 0 & B_{co} & 0 & B_{24} \\ 0 & 0 & B_{\overline{co}} & B_{34} \\ 0 & 0 & 0 & B_{\overline{c}o} \end{bmatrix} \end{equation}
\begin{equation} \hat{x}_{0,0} = \begin{bmatrix} x_{c\overline{o}} \\ x_{co} \\ 0 \\ 0 \end{bmatrix}, \hat{C} = \begin{bmatrix} 0 & C_{co} & 0 & C_{\overline{c}o} \end{bmatrix} \end{equation}
The minimal realization of the state space model, which is the part of the system that is controllable and observable is given by \((A_{co},B_{co},C_{co})\) and has initial state \(x_{co}\).
% ** Calculating the Kalman decomposition and minimal realization
The calculation of the Kalman decomposition can be performed by using the singular value decomposition of the controllability and observability matrices. We denote this singular value decomposition of both matrices by
\begin{equation} \obs = \begin{bmatrix} U_0 & U_1 \end{bmatrix} \begin{bmatrix} \sigma_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} V_0^T \\ V_1^T \end{bmatrix},~ X = \begin{bmatrix} G_0 & G_1 \end{bmatrix} \begin{bmatrix} \rho_0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} H_0^T \\ H_1^T \end{bmatrix} \end{equation}
Due to the orthogonal condition of the singular vectors, we have that \(\obs V_1 = 0\). All vectors which lie in the right null space of the observability matrix, are by definition non-observable. The columns of \(V_1\) form an orthogonal basis for the non-observable part of the system.
To find a basis of the controllable or reachable part of the system we calculate a numerical basis for the column space of the observability matrix. This is, by definition, a basis of the space of all reachable states. From the properties of the singular value decomposition it follows that \(G_0\) is such a basis. We can thereby conclude that
\begin{equation} G_0 = \begin{bmatrix} T_{c\overline{o}} & T_{co} & \end{bmatrix}, V_1 = \begin{bmatrix} T_{c\overline{o}} & T_{\overline{co}} & \end{bmatrix} \end{equation}
The four spaces \(T_{co}\), \(T_{\overline{c}o}\), \(T_{c\overline{o}}\) and \(T_{\overline{co}}\) can now be calculated as
- \(T_{c\overline{o}}\) is found by calculating the intersection between \(V_1\) and \(G_0\).
- \(T_{\overline{co}}\) is found by calculating the complement of \(T_{c\overline{o}}\) in \(V_1\).
- \(T_{co}\) is found by calculating the complement of \(T_{c\overline{o}}\) in \(G_0\).
- \(T_{\overline{c}o}\) is found by calculating the complement of \(\begin{bmatrix} T_{c\overline{o}} & T_{\overline{co}} & T_{co} \end{bmatrix}\) in \(\real^m\).
The transformed system matrices, presented in Equations~\eqref{eqn:2R-kalman-dec1} and~\eqref{eqn:2R-kalman-dec1} can now be calculated together with the minimal realization.
Modal analysis of commuting state space models
The modal analysis of a two-dimensional commuting state space model is based on the generalized eigenvalue decomposition of commuting matrices as defined in Definition~\ref{def:ch1-gen-eigenbasis} from Chapter~\ref{ch:linear-algebra}. In this section we will proof that with every generalized eigenvector, an eigenmode of the system can be associated, similar as for one-dimensional state space models. This derivation is based on the properties of the Jordan chain formed by every generalized eigenvector.
The shared eigenvector of commuting matrices
Every pair of commuting matrices does have at least one shared eigenvector (Lemma 1.3.19)~\cite{horn2012matrix}. We start the modal analysis by focusing on this shared eigenvector, the full analysis is later carried out by using the generalized eigenbasis for commuting matrices, presented in Theorem~\ref{def:ch1-gen-eigenbasis} of Chapter~\ref{ch:linear-algebra}. Consider the commuting state space model \((C,A,B)\) with initial state \(x\in\real^m\). We assume that this state is a shared eigenvector of both system matrices, with eigenvalues \(\gamma\) and \(\lambda\) respectively for matrices \(A\) and \(B\). From the properties of eigenvectors it follows that
\begin{equation} A^kB^l x = A^k(\lambda^lx) = \lambda^lA^kx = \lambda^l\gamma^kx. \end{equation}
For this initial state, the output of the system is thus equal to
\begin{equation} y[k,l] = C A^k B^l x = \lambda^l\gamma^k Cx. \end{equation}
This shows that the eigenvalues of both system matrices determine the dynamics of the system.
In an extreme case, we assume that both system matrices can be simultaneously diagonalized, such that there exists a basis \(X = \left\lbrace x_1, x_2, \dots, x_m\right\rbrace\) of \(\real^m\) for which
\begin{equation} Ax_i = \gamma_i x_i,~Bx_i = \lambda_i x_i, \end{equation}
for all values of \(1\leq i\leq m\). The values of \(\gamma_k\) and \(\lambda_k\) are respectively the eigenvalues of \(A\) and \(B\). Given a random initial vector \(x\) which has coordinates \(\alpha_1,\dots,\alpha_m\) in the basis \(X\), i.e.
\begin{equation} x = \sum_{i=1}^{m} \alpha_i x_i. \end{equation}
We can calculate the output of the two dimensional state space model by multiplying the powers of both system matrices with this expression. This yields
\begin{equation} y[k,l] = CA^kB^lx = \sum_{i=1}^{m}\alpha_i C A^k B^l x_i = \sum_{i=1}^{m}\alpha_i \gamma_i^k \lambda_i^l Cx_i. \end{equation}
The general case
In general it is not possible to simultaneously diagonalize both system matrices to find a common eigenbasis. To generalize the previous results, we use the generalized eigenbasis for commuting matrices, as defined in Definition~\ref{def:ch1-gen-eigenbasis} from Chapter~\ref{ch:linear-algebra}.
Consider the commuting state space model \((C,A,B)\) with an initial state \(x\in\real^m\). Let \(X = \left\lbrace x_1, x_2, \dots, x_m\right\rbrace\) be the generalized eigenbasis for both commuting matrices. We will first calculate the output of the system when the initial state is equal to a single generalized eigenvector. The general result is later obtained by taking a suitable linear combination of the eigenvectors and the associated solution.
Assume that the initial state \(x\) is equal to \(x_i\in X\) for some index \(1\leq i \leq m\). By definition, this vector satisfies
\begin{equation} \label{eqn:2DR-geneigenbasis1} \begin{matrix} (\eye\lambda_i-A)^{n_i} x_i = 0 \\ (\eye\gamma_i-B)^{m_i} x_i = 0, \\ \end{matrix} \end{equation}
and
\begin{equation} \label{eqn:2DR-geneigenbasis2} \begin{matrix} (\eye\lambda_i-A)^{n_i-1} x_i \neq 0 \\ (\eye\gamma_i-B)^{m_i-1} x_i \neq 0 \\ \end{matrix} \end{equation}
for some values \(\lambda_i\) and \(\gamma_i\) and some integers \(n_i\) and \(m_i\).
To simplify the notation in the further derivation of the model decomposition, we temporally drop the subscript \(i\). In this way we have that \(x_i=x,m_i = \mu\) and \(n_i = \nu=\)
The value of the state at multi index \(k,l\geq 0\) is than
\begin{equation} x[k,l] = A^k B^l x. \end{equation}
Because \(x\) is by definition a generalized eigenvector of \(B\), we have that
\begin{equation} B^l x = \sum_{j=1}^{\mu} \binom{l}{\mu-j}\gamma^{l-\mu+j}(B-\gamma\eye)^{\mu-j} x. \end{equation}
When multiplying both sides by \(A^k\) from the left we get
\begin{equation} x[k,l] = A^k B^l x_i = \sum_{j=1}^{\mu} \binom{l}{\mu-j}\gamma^{l-\mu+j}(B-\gamma\eye)^{\mu-j} \left(A^kx\right). \end{equation}
Because the vector \(x_i\) is also a generalized eigenvector of \(A\), we can rewrite the expression for \(A^kx_i\) as
\begin{equation} A^kx = \sum_{h=1}^{\nu} \binom{k}{\nu-h}\lambda^{k-\nu+h}(A-\lambda\eye)^{\nu-h} x. \end{equation}
The combined expression of the \(x[k,l]\) is
\begin{multline}\label{eqn:modal_2d} x[k,l] = \sum_{h=1}^{\nu}\sum_{j=1}^{\mu} \binom{l}{\mu-j}\binom{k}{\nu-h} \\ \lambda^{k-\nu+h}\gamma^{l-\mu+j}(B-\gamma\eye)^{\mu-j}(A-\lambda\eye)^{\nu-h}x. \end{multline}
With every generalized eigenvector of Theorem~\ref{thm:commuting} we can associate such an eigenmode. The total output is a linear combination of these modes, depending on the value of the output matrix and the initial state.
Example
To clarify these ideas, we calculate the solution of the state vector as a function of the generalized eigenvalues and eigenvectors for two commuting matrices \(A\) and \(B\)
\begin{equation} A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\ \end{bmatrix}, B = \begin{bmatrix} 2 & 0 & 1 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix}. \end{equation}
These matrices have been used previously in Section~\ref{sec:intro-example-commuting} of Chapter~\ref{ch:linear-algebra} The generalized eigenvectors are given by the standard normal basis vectors of \(\real^3\), denoted by \(x_1, x_2\) and \(x_3\). The powers of the matrices \(A\) and \(B\) are given by
\begin{equation} A^k = \begin{bmatrix} 1 & k & k(k-1)/2 \\ 0 & 1 & k \\ 0 & 0 & 1 \end{bmatrix}, B^l = \begin{bmatrix} 2^l & 0 & l2^{l-1} \\ 0 & 2^l & 0 \\ 0 & 0 & 2^l \end{bmatrix}. \end{equation}
The vector \(x_1\) is an eigenvector of both matrices \(A\) and \(B\), and we have that
\begin{equation} A^k B^l x_1 = 2^lx_1, \end{equation}
which is consistent with the formula of Equation~\eqref{eqn:modal_2d}, with \((\mu,\nu)=(1,1)\). The vector \(x_2\) is an eigenvector of \(B\) and has the property that \((B-2\eye)x_2=0\). When applying \(A^k\) to this vector we get
\begin{equation} A^k x_2 = k x_1 + x_2. \end{equation}
The right hand side of the equation is a linear combination of two eigenvectors of the matrix \(B\) and thus
\begin{equation} B^lA^k x_2 = B^l(k x_1 + x_2) = 2^l(k x_1 + x_2). \end{equation}
This is consistent with Equation~\eqref{eqn:modal_2d} for \((\mu,\nu)=(2,1)\), \(\lambda=1\) and \(\gamma=2\). For the last vector, \(x_3\) we have that
\begin{equation} A^k x_3 = \frac{k(k-1)}{2}x_1 + k x_2 + x_3. \end{equation}
The vectors \(x_1\) and \(x_2\) are eigenvectors of \(B\) and \(B^lx_3 = l2^{l-1}x_1 + 2^lx_3\). We thus get
\begin{equation}\label{eqn:asthpyp85473946} B^lA^k x_3 = B^l(\frac{k(k-1)}{2}x_1 + k x_2) + B^lx_3 = 2^l(\frac{k(k-1)}{2}x_1 + k x_2) + l2^{l-1}x_1 + 2^lx_3. \end{equation}
Let us compare this result explicitly with Equation~\eqref{eqn:modal_2d} for \((\mu,\nu)=(3,2)\), \(\lambda=1\) and \(\gamma=2\). The double sum of Equation~\eqref{eqn:modal_2d} up to \((\mu,\nu)\) has a total of 6 terms. The values of every term in the sum are explicitly calculated and shown in Table~\ref{tbl:example_calc}, together with the simplified expression in the right column. The sum of all simplified terms is exactly equal to the expression in Equation~\eqref{eqn:asthpyp85473946}.
\begin{table} \centering \caption[Example calculations.]{Explicit calculation of the individual terms in the sum of Equation~\eqref{eqn:modal_2d} for the various indices. These calculations are used in the example of Section~\ref{sec:example_modal}}\label{tbl:example_calc} \begin{tabular}{ c c c c } \toprule $i$ & $j$ & Term in the sum & Simplified expression \\ \midrule 1 & 1 & $\binom{k}{2}\binom{l}{1}2^{l-1}(B-2\eye)(A-\eye)^2x_{3}$ & 0 \\ 1 & 2 & $\binom{k}{2}\binom{l}{0}2^{l}(A-\eye)^2x_{3}$ & $2^l\frac{k(k-1)}{2}x_{1}$ \\ 2 & 1 & $\binom{k}{1}\binom{l}{1}2^{l-1}(B-2\eye)(A-\eye)x_{3}$ & $0$ \\ 2 & 2 & $\binom{k}{1}\binom{l}{0}2^{l}(A-\eye)x_{3}$ & $2^{l}kx_{2}$ \\ 3 & 1 & $\binom{k}{0}\binom{l}{1}2^{l-1}(B-2\eye)x_{3}$ & $l2^{l-1}x_{1}$ \\ 3 & 2 & $\binom{k}{0}\binom{l}{0}2^{l}x_{3}$ & $2^lx_{3}$ \\bottomrule \end{tabular} \end{table}
Conclusions
In this chapter we introduced the class of commuting state space models. The two fundamental theorems that govern this model class, is the theorem of Cayley–Hamilton for commuting matrices and the existence of a set of generalized eigenvectors for commuting matrices. The theorem of Cayley–Hamilton was first used to derive a set of difference equations which satisfy the dynamic equations of the state space model. Secondly, Cayley–Hamilton was used to derive the observability matrix and the recursive observability matrix.
We concluded this chapter by deriving an expression for the modal solution of a commuting state space model.