In this chapter we introduce one-dimensional singular system, also known as descriptor systems or differential algebraic equations (\gls{DAE})~\cite{brenan1996numerical}. A descriptor system is an extension of the classical state space model, as presented in the previous chapter and is characterized by a causal and non-causal solution, running forward and backward in time respectively (see e.g.~\cite{moonen1992subspace}). The causal part is linked to the finite roots of the characteristic equation associated with the descriptor system and the non-causal part is linked to roots at infinity.
Descriptor systems
A singular state space model for discrete systems is characterized by the following equation
\begin{equation}\label{eqn:1S-SS} \begin{aligned} Ex[k+1] = & Ax[k] \\ y[k] = & C x[k], \end{aligned} \end{equation}
where \(y[k] \in \real^q\) and \(x[k] \in \real^m\) are the output and the state vector of the system respectively. The first equation is called the state update equation, updating the state at every index \(k\), whereas the second equation is the output equation, relating the internal state and the output. The matrices \(E\) and \(A\) are both elements of \(\complex^{m\times m}\), and \(k\) is the discrete time index. When the matrix \(E\) is singular, this system is called a descriptor system~\cite{verghese1981generalized}. When \(E\) is a regular matrix, we can multiply the state update equation from the left by the matrix \(E^{-1}\) to obtain a regular one-dimensional system. The system properties are determined by the linear matrix pencil $(A,E)$~\cite{golub13}, which must be regular. Meaning that \(\det(sE-A)\) is not identically zero, which implies that there exists at least one complex value \(\mu\) such that \(\mu E-A\) is invertible.
A descriptor system is unique modulo a left and right non-singular transformation. If we change the basis in which we represent the state vector by introducing a new state vector \(z[k]\) such that
\begin{equation} x[k]= Qz[k], \end{equation}
where \(Q \in \real^{m \times m}\) is an invertible matrix, we have that \(EQQ^{-1}x[k+1] = AQQ^{-1}x[k]\) and thus
\begin{equation} \begin{aligned} EQz[k+1] = & AQz[k] \\ y[k] = & C Qz[k]. \end{aligned} \end{equation}
The above state space model can further be changed by pre-multiplying the state update equation by a matrix \(P\in\real^{m\times m}\). The final model is
\begin{equation}\label{eqn:1S_weier} \begin{aligned} PEQz[k+1] = & PAQz[k] \\ y[k] = & C Qz[k]. \end{aligned} \end{equation}
This demonstrates that both singular state space models from Equation~\eqref{eqn:1S-SS} and Equation~\eqref{eqn:1S_weier} are in fact the same system and both representations can be used in the further analysis of this model class.
The fact that descriptor systems are only uniquely defined modulo a left and right non-singular matrix multiplications will be utilized in the next section to place the state space model in the Weierstrass canonical form.
Generalized eigenvalue problem
The properties of a descriptor system are determined by the generalized eigenvalues of the matrix pencil \((A,E)\). The vector \(x_i \neq 0\) is an eigenvector of the matrix pencil if and only if
\begin{equation}\label{eqn:1_desc} (Es_i - A \gamma_i)x_i = 0 \end{equation}
for some values of \((s_i,\gamma_i)\in \complex^{2}\). This pair is the called the generalized eigenvalue of the eigenvector \(x_i\). If \(\gamma_i\) is equal to zero and \(s_{i}\neq 0\), we say that the system has a pole at infinity. Both values of \(s_i\) and \(\gamma_i\) can not simultaneous be zero, otherwise the pencil \((Es_i - A \gamma_i)\) is identically zero.
To get an intuition with this notion of `a pole at infinity’ we will first analyze the possible solutions. Assume that the values \((s_i,\gamma_i)\) and the vector \(x_i\) are a solution of Equation~\eqref{eqn:1_desc}. There are two possible outcomes, either \(\gamma_i\) is equal to zero or it is not. We can rewrite the pair \((s_i,\gamma_i)\) for the latter case, where \(\gamma_i\neq 0\), as \((s_i/\gamma_i,1)\). Notice that this pair is still a valid solution for the given generalized eigenvalue problem. In the other case where \(\gamma_i\) is 0 the solution has the form \((s_i,0)\), which can be transformed to \((1,0)\) via a division by \(s_i\).
This effectively results in two different kinds of solutions, either the generalized eigenvalues can be transformed to \((\lambda_i,1)\) or \((1,0)\). The first kind of solutions are called finite eigenvalues, and the second class are solutions at infinity. Solutions at infinity occur if and only if the matrix \(E\) from Equation~\eqref{eqn:1_desc} is rank deficient.
To see why the matrix pencil, and the generalized eigenvalues, are important to quantify the behavior of a descriptor system, we take the generalized eigenvector \(x_i\) which is associated with the generalized eigenvalue \((\lambda_i,1)\). Assume that the initial state of the system, denoted by \(x[0]\), is equal to this generalized eigenvector. The solution of the state sequence is then equal to
\begin{equation} x[k] = \lambda^k x_i = \lambda x[k-1]. \end{equation}
This can be verified by plugging this solution back into the state space model.
Now consider the generalized eigenvector \(x_i\) which is associated with the generalized eigenvalue \((1,0)\). From the definition of the generalized eigenvectors it follows that \((E - A 0)x_i = 0\), and thus \(Ex_i = 0\). The generalized eigenvectors of the matrix pencil, associated with a solution at infinity lie in the null space of the matrix \(E\).
The Weierstrass canonical form
Closely related to the generalized eigenvalue problem is the Weierstrass Canonical Form (WCF) of a matrix pencil~\cite{gantmacher1960theory}, which states that for every regular matrix pencil there exist matrices \(P\), \(Q\) of full rank where
\begin{equation}\label{eqn:1S-wcf} P(Es-A)Q = \begin{bmatrix}\eye & 0 \\ 0 & N\end{bmatrix}s - \begin{bmatrix}A_{R} & 0 \\ 0 & \eye \end{bmatrix} = \bar{E}s - \bar{A}, \end{equation}
with \(\eye\) the identity matrix. The dimension of \(A_{R}\) correspond to the dimension of the identity matrix in \(\bar{E}\), the same applies to the matrix \(N\), which has the same dimensions as the identity matrix in \(\bar{A}\). The matrix \(N\) is a nilpotent matrix, which can be further reduced to a Jordan form and the matrix \(A_{R}\) is a matrix which can also be put in a Jordan canonical form via a basis transformation. A nilpotent matrix is a matrix with the property that, for some positive integer \(k\), the matrix \(N^k\) becomes identically zero, i.e.~all elements of the matrix are zero. The smallest positive integer \(k\) for which this is the case is called the nilpotency index of a matrix. The eigenvalues of this matrix are all exactly zero.
% Note that a matrix pencil in the WCF is also a commuting matrix pencil.
State sequence
The state sequence of a descriptor system has been derived in~\cite{moonen1992subspace}. In this thesis we follow a different approach and derive a novel and more general expression for the state sequence. The obtained result is slightly different from the presented results in~\cite{moonen1992subspace}. In Section~\ref{sec:1S-comparison} we will compare both results and discuss the differences.
To start our discussion, we first formally define the concept of a finite state sequence.
For the given descriptor system presented in Equation~\eqref{eqn:1S-SS} and some finite horizon \(n\), we define the finite state sequence \(x[k]\) for \(0\leq k \leq n\) as the state sequence that satisfies the dynamic equation of the descriptor system.
Infinite state sequences are not considered in this thesis as the non-causal effects of the descriptor system only affect finite state sequences. The most important implication of working on a finite horizon, where the state \(x[k]\) is only defined for \(0\leq k\leq n\) is to note that \(x[n+1]\) does not exist. It therefore does not make any sense to write
\begin{equation} Ex[n+1] = Ax[n], \end{equation}
because the left hand side of this equation simply does not exist.
Commuting matrix pencils
Consider the regular, commuting matrix pencil \((A,E)\) of size \(m\times m\) and output matrix \(C\), regular, meaning that \(\det(Es-A)\) is not identically zero, and commuting, meaning that both matrices \(A\) and \(E\) commute. This class of matrix pencils has been introduced in Chapter~\ref{ch:linear-algebra}. We consider the state sequence over a finite horizon such that \(x[k]\) is only defined for \(0\leq k\leq n \leq \infty\). In this case, we show that state sequence is given by
\begin{equation} x[k] = A^k E^{n-k} x, \end{equation}
for some vector \(x\). We call the vector \(x\) the generalized state vector. It is clear that \(x[k]\) satisfies the dynamic equation of the descriptor system as
\begin{equation} Ex[k+1] = E (A^{k+1} E^{n-k-1} x) = A (A^k E^{n-k} x) = Ax[k]. \end{equation}
This equation is however only valid for \(0\leq k \leq n-1\), as the expression contains the value \(x[k+1]\). The initial state of the system is then equal to \(x[0] = E^n x\) and the final state is \(x[n] = A^nx\). The output of the system is
\begin{equation} y[k] = C A^k E^{n-k} x. \end{equation}
We will introduce a shorthand notation for the expression \(A^k E^{n-k}\) and introduce the evolution operator, as it is used a lot in the following sections.
Given the commuting matrix pencil \((A,E)\) and two positive finite natural numbers \(p,n\) with \(p\leq n\). We define \((A,E)^p_n\) as
\begin{equation} (A,E)^p_n = A^p E^{n-p} \end{equation}
We can go one step further and use the shorthand notation \(\mathcal{A} = (A,E)\), such that
\begin{equation} \mathcal{A}^p_n = A^p E^{n-p}. \end{equation}
This notation is called the evolution operator.
By using this notation, we can write the output of a descriptor system over a finite horizon \(n\) as
\begin{equation} y[k] = C \mathcal{A}^k_n x, \end{equation}
which simplifies the solution and is reminiscent of the notation for regular systems. Using the evolution operator will further draw out the similarities between regular systems and descriptor systems, with the intent to later define a single realization algorithm that can estimate both model classes. This operator behaves well under multiplication, we have that
\begin{equation} \mathcal{A}^k_n \mathcal{A}^l_m = A^k E^{n-k} A^l E^{m-l} = A^{k+l} E^{n+m-(k+l)}=\mathcal{A}^{k+l}_{n+m}. \end{equation}
The effects of multiplying by \(E\) and \(A\) can also explicitly be written out. We have that
\begin{equation} \mathcal{A}^k_n A = (A^{k}E^{n-k})A = A^{k+1}E^{n+1-(k+1)} = \mathcal{A}^{k+1}_{n+1}, \end{equation}
and
\begin{equation} \mathcal{A}^k_n E = (A^{k}E^{n-k})E = A^{k}E^{n+1-k} = \mathcal{A}^{k}_{n+1}. \end{equation}
The state sequence in the WCF
Consider the matrix pencil \((A,E)\), which is placed in the WCF. We can write
\begin{equation} A = \begin{bmatrix} A_{R}& 0 \\ 0 & \eye \end{bmatrix}, E = \begin{bmatrix} \eye & 0 \\ 0 & N\end{bmatrix}. \end{equation}
It is clear that both matrices commute because
\begin{equation} AE = \begin{bmatrix} A_{R}& 0 \\ 0 & N \end{bmatrix} = EA. \end{equation}
This commutation allows us to use the results derived in Section~\ref{sec:1S-state-commuting} to find an expression for the output and state sequence of a descriptor system which is placed in the WCF. For the finite horizon \(n\), the state sequence is equal to
\begin{equation} x[k] = \mathcal{A}_n^k x = \begin{bmatrix} A_{R}^k& 0 \\ 0 & N^{n-k} \end{bmatrix}x. \end{equation}
This block structure allows us to partition both the generalized state vector \(x\) and the state vector \(x[k]\) in two distinct parts and write
\begin{equation} \begin{bmatrix} x_r[k] \\ x_s[k] \end{bmatrix} = \begin{bmatrix} A_{R}^k& 0 \\ 0 & N^{n-k} \end{bmatrix} \begin{bmatrix} x_r \\ x_s \end{bmatrix}. \end{equation}
The initial state of the system is then equal to
\begin{equation} \begin{bmatrix} x_r[0] \\ x_s[0] \end{bmatrix} = \begin{bmatrix} A_{R}^0& 0 \\ 0 & N^{n} \end{bmatrix} \begin{bmatrix} x_r \\ x_s \end{bmatrix} = \begin{bmatrix} A_{R}^0 x_r \\ N^nx_s \end{bmatrix}. \end{equation}
Which proves that \(x_r=x_r[0]\), as \(A_{R}^0=\eye\). On the other hand, the final state of the system is given by
\begin{equation} \begin{bmatrix} x_r[n] \\ x_s[n] \end{bmatrix} = \begin{bmatrix} A_{R}^n& 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x_r \\ x_s \end{bmatrix} = \begin{bmatrix} A_{R}^nx_r \\ x_s \end{bmatrix}, \end{equation}
proving that \(x_s[n] = x_s\). Using both results we find that
\begin{equation} \begin{bmatrix} x_r[k] \\ x_s[k] \end{bmatrix} = \begin{bmatrix} A_{R}^kx_r[0] \\ N^{n-k}x_s[n] \end{bmatrix}. \end{equation}
If we partition the output matrix \(C\) in the same way and write \(C=[C_r~C_s]\), we get
\begin{equation}\label{eqn:1S-SS-WCF-solution} y[k] = C_r x_r[k] + C_s x_s[k] = C_r A_r^k x_r[0] + C_s N^{n-k} x_s[n]. \end{equation}
Comparison with classical derivation
An expression for the output of a descriptor system was previously derived in~\cite{moonen1992subspace}. The authors in this work concluded in a footnote that the singular part of the state vector is never observable as a result of a slightly different output matrix than the one presented in Equation~\eqref{eqn:1S-SS-WCF-solution}. The reason for this discrepancy is a boundary error in the derivation of their results.
The authors of~\cite{moonen1992subspace} start by placing the descriptor system in the WCF
\begin{equation}\label{eqn:moonen_1} \begin{bmatrix} \eye & 0 \\ 0 & N\end{bmatrix} \begin{bmatrix} x_{R}[k+1] \\ x_{S}[k+1] \end{bmatrix} = \begin{bmatrix} A_{R}& 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x_{R}[k] \\ x_{S}[k] \end{bmatrix}, \end{equation}
\begin{equation} y[k] = \begin{bmatrix} C_{R} & C_{S} \end{bmatrix}\begin{bmatrix} x_{R}[k] \\ x_{S}[k] \end{bmatrix}. \end{equation}
The block structure of Equation~\eqref{eqn:moonen_1} effectively decouples the singular part of the state vector and the regular part and we get two equations which are independent of each other. This independence allows us to transform Equation~\eqref{eqn:moonen_1} into
\begin{equation}\label{eqn:descriptor_step1} \begin{bmatrix} \eye & 0 \\ 0 & \eye\end{bmatrix} \begin{bmatrix} x_{R}[k+1] \\ x_{S}[k] \end{bmatrix} = \begin{bmatrix} A_{R}& 0 \\ 0 & N\end{bmatrix} \begin{bmatrix} x_{R}[k] \\ x_{S}[k+1] \end{bmatrix}, \end{equation}
by switching the singular part of the equation to the other side of the equality sign. The right hand side of the equality now depends on both indices \(k\) and \(k+1\). We introduce a new state vector \(x_{S}[k] = \tilde{x}_{S}[k-1]\) such that the right hand side of the equality only depends on the index \(k\). Here the authors of~\cite{moonen1992subspace} make a small mistake as they define \(k\) as \(0 \leq k \leq n\), and therefore introduce the non-existent value of \(x_s[n+1]\) in the equation. The vector \(x_S[k]\) is only defined up to \(k\) equal to \(n\), therefore we have that \(\tilde{x}_{S}[l]\) is only defined for \(-1\leq l \leq n-1\).
Substituting \(\tilde{x}_{S}[k]\) in to Equation~\eqref{eqn:descriptor_step1} gives
\begin{equation} \begin{bmatrix} x_{R}[k+1] \\ \tilde{x}_{S}[k-1] \end{bmatrix} = \begin{bmatrix} {A}_{R}& 0 \\ 0 & N\end{bmatrix} \begin{bmatrix} x_{R}[k] \\ \tilde{x}_{S}[k] \end{bmatrix}, \end{equation}
\begin{equation} y[k] = \begin{bmatrix} C_{R} & C_{S}N \end{bmatrix}\begin{bmatrix} x_{R}[k] \\ \tilde{x}_{S}[k] \end{bmatrix}. \end{equation}
For \(0\leq k \leq n-1\), the output of this model is equal to
\begin{equation}\label{eqn:solution_descriptor1} y[k] = C_{R}A_{R}^{k}x_{R}[0] + C_{S}N^{n-k}\tilde{x}_{S}[n-1]. \end{equation}
From equation~\eqref{eqn:moonen_1} we can find the output at index \(k=n\), which is
\begin{equation}\label{eqn:solution_descriptor2} y[n] = C_{R}A_{R}^{n}x_{R}[0] + C_{S}{x}_{S}[n]. \end{equation}
Combining both expressions in Equations~\eqref{eqn:solution_descriptor1} and~\eqref{eqn:solution_descriptor2}, we find that
\begin{equation} y[k] = C_{R}A_{R}^{n}x_{R}[0] + C_{S}N^{n-k}{x}_{S}[n], \end{equation}
for all values of \(0\leq k \leq n\), whereas~\cite{moonen1989and} wrongly finds
\begin{equation} y[k] = C_{R}A_{R}^{n}x_{R}[0] + C_{S}N^{n-k+1}{x}_{S}[n] \end{equation}
Both results differ by a single multiplication of \(N\) in the singular part.
The theorem of Cayley–Hamilton
% ** The characteristic equation of a matrix pencil The characteristic equation of a matrix pencil is defined as follows~\cite{chang1992generalized}.
The characteristic equation of the regular matrix pencil \((A,E)\) of size \(m\times m\) is defined as
\begin{equation} \Delta(s) = \det(sE-A). \end{equation}
% ** The theorem of Cayley–Hamilton for standard pencils The theorem of Cayley–Hamilton for matrix pencils is given below:
The standard pencil \((A,E)\) of size \(m \times m\) satisfies its own characteristic equation; that is, \(\Delta(A,E)=0\), where
\begin{equation} \Delta(s) = \det(sE-A) = \sum_{k=0}^{m}\alpha_k s^k. \end{equation}
The expression \(\Delta(A,E)\) is equal to
\begin{equation} \Delta(A,E) = \sum_{k=0}^{m}\alpha_k A^kE^{m-k}. \end{equation}
Using the evolution operator from Definition~\ref{defn:1DS-evolution}, we have
\begin{equation} \Delta(A,E) = \Delta(\mathcal{A})=\sum_{k=0}^{m}\alpha_k \mathcal{A}^k_m = 0. \end{equation}
Using the the evolution operator further exemplifies the parallels with the theorem of Cayley–Hamilton for regular systems, as formulated in Theorem \ref{thm:1DR-ch}.
This result was proven in~\cite{chang1992generalized}, we will not repeat this proof here. In Chapter~\ref{ch:2DS}, we proof the generalized result for two-dimensional descriptor systems.
Difference equation
The first result that can be derived from the generalized theorem of Cayley–Hamilton is the calculation of the difference equation associated to the descriptor system from Equation~\eqref{eqn:1S-SS}. Given a descriptor system with generalized state \(x\), output matrix \(C\) and the standard pencil \((A,E)\) of size \(m\times m\). According to Theorem~\ref{thm:1S-general-ch} we have that
\begin{equation}\label{eqn:1S-ch-example} \Delta(A,E) = \Delta(\mathcal{A})=\sum_{k=0}^{m}\alpha_k \mathcal{A}^k_m = 0. \end{equation}
Pre and post multiplying this expression respectively by \(C\) and \(x\) we get
\begin{equation} C\Delta(A,E)x =\sum_{k=0}^{m}\alpha_k C\mathcal{A}^k_mx = \sum_{k=0}^{m} \alpha_k y[k] = 0, \end{equation}
which has the same form as for regular systems. Note that this difference equation can only be applied to the first \(m\) points in the time series \(y[k]\). To derive a more general result, we have to transform the standard pencil to its WCF form. Take
\begin{equation} E = \begin{bmatrix} \eye & 0 \\ 0 & N\end{bmatrix},~ A = \begin{bmatrix} A_{R}& 0 \\ 0 & \eye \end{bmatrix},~ C = \begin{bmatrix} C_R & C_S \end{bmatrix}, x = \begin{bmatrix} x_r[0] \\ {x}_s[n] \end{bmatrix}, \end{equation}
for some value \(n\). The state vector at index \(l\) is \(x[l] = \mathcal{A}^l_n x\). Pre and post multiplying Equation~\eqref{eqn:1S-ch-example} respectively by \(C\) and \(x[l]\) we get
\begin{equation} C\Delta(A,E)x[l] =\sum_{k=0}^{m}\alpha_k C\mathcal{A}^k_m\mathcal{A}^l_n x = \sum_{k=0}^{m} \alpha_k \mathcal{A}^{k+l}_{n+m}x = 0. \end{equation}
The expression of \(C\mathcal{A}^{k+l}_{n+m} x\) simplifies as
\begin{equation} \begin{aligned} C\mathcal{A}^{k+l}_{n+m}x = &~\begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} A_{R}^{k+l} & 0 \\ 0 & N^{n+m-(k+l)} \end{bmatrix} \begin{bmatrix} x_r[0] \\ {x}_s[n]. \end{bmatrix} \\ = &~C_RA_R^{k+l}x_R[0] + C_SN^{n+m-(k+l)} {x}_S[n]. \end{aligned} \end{equation}
Plugging this expression back in to the difference equation results in
\begin{equation} 0 =\sum_{k=0}^{m}\alpha_k y_r[k+l] + \sum_{k=0}^{m}\alpha_k C_SN^{n+m-(k+l)} {x}_S[n]. \end{equation}
This difference equation reveals the structure of the solution of a descriptor system. For small positive values of \(k+l\) the expression \(N^{n+m-(k+l)}\) will be zero and the difference equation is determined by the causal dynamics. When \(k+l\) increases, the non causal state changes the difference equation and enters the equation as if it were an input signal.
Observability
In this section we discuss the observability of descriptor systems. Two equivalent theorems to test the observability are provided, one theorem that uses the observability matrix for descriptor systems and the extended theorem of Popov–Belevitch–Hautus.
The observability matrix
The observability of regular linear state space models has been discussed in the previous chapter, where we showed that a system was observable if we can estimate the initial state. In the case of descriptor systems, the output is not only determined by the initial state but is also affected, in a non-causal way, by the final value of the singular part of the state vector. We have combined both states by introducing the generalized state \(x\) of the descriptor system. The observability matrix for the descriptor system parameterized by the regular, commuting pencil \((A,E)\) of size \(m\times m\) and output matrix \(C\) is
\begin{equation} \obs = \begin{bmatrix} C E^{m-1} \\ C A^{1}E^{m-2} \\ \vdots \\ C A^{m-2}E^{1} \\ C A^{m-1} \\ \end{bmatrix} = \begin{bmatrix} C \mathcal{A}^{0}_{m-1} \\ C \mathcal{A}^{1}_{m-1} \\ \vdots \\ C \mathcal{A}^{m-2}_{m-1} \\ C \mathcal{A}^{m-1}_{m-1} \end{bmatrix}. \end{equation}
The relation between the output of the system and the observability matrix is
\begin{equation} \begin{bmatrix} y[0] \\ y[1] \\ \vdots \\ y[m-1] \\ \end{bmatrix} = \obs x. \end{equation}
The generalized state \(x\) can be estimated if and only if the observability matrix is of full rank. This is summarized in the Theorem~\ref{thm:aosntuhaosetnhucc}. When the generalized state of the system is known, the entire state sequence can be calculated as
\begin{equation} x[k] = \mathcal{A}^{k}_{m-1}x = A^k E^{m-1-k}x \end{equation}
The state space model from Equation~\eqref{eqn:1S-SS} with \(q\) outputs and a $m$-dimensional state vector, parameterized by the regular, commuting matrix pencil \((A,E)\) and output matrix \(C\), is observable if and only if the observability matrix
\begin{equation} \obs = \begin{bmatrix} C \mathcal{A}^{0}_{m-1} \\ C \mathcal{A}^{1}_{m-1} \\ \vdots \\ C \mathcal{A}^{m-2}_{m-1} \\ C \mathcal{A}^{m-1}_{m-1} \end{bmatrix}, \end{equation}
has full rank.
When the system is placed in the Weierstrass canonical form, the observability matrix is equal to
\begin{equation}\label{eqn:obs-no-gap} \obs = \begin{bmatrix} C_R & C_S N^{m-1} \\ C_R A_R & C_S N^{m-2} \\ \vdots & \vdots \\ C_R A_R^{m-2} & C_SN \\ C_R A_R^{m-1} & C_S \end{bmatrix} = \begin{bmatrix} \obs_R & \obs_S \end{bmatrix}, \end{equation}
which is equal to the concatenation of two matrices \(\obs_R\) and \(\obs_S\). The first matrix is the observability matrix for the causal subsystem of the descriptor system whereas the second matrix \(\obs_S\), is the observability matrix for the non-causal dynamics. Note that the powers of \(N\) decrease for an increasing row index.
Column compression
When the descriptor system is not observable, we can calculate the observable part by using a column compression on the columns of the observability matrix. The algorithm discussed in Chapter~\ref{ch:1DR} can be used in this case. When the system is placed in the WCF, special care has to taken to preserve the structure of the observability matrix by keeping the columns of \(\obs_R\) and \(\obs_S\) separated. To apply the column compression in this case, whilst preserving the WCF of the descriptor system, we write the observability matrix as two separate matrices, one containing the columns of the regular part and the other one containing the columns of the singular part. In this way we get two matrices
\begin{equation} \obs_R = \begin{bmatrix} C_R \\ C_R A_R \\ \vdots \\ C_R A_R^{m-2} \\ C_R A_R^{m-1} \end{bmatrix},~\obs_S = \begin{bmatrix} C_S N^{m-1} \\ C_S N^{m-2} \\ \vdots \\ C_SN \\ C_S \end{bmatrix}, \end{equation}
and \(\obs = \begin{bmatrix}\obs_R & \obs_S\end{bmatrix}\). Both matrices can now be compressed individually via a column compression. These compressions can be computed in the same way as before and result in two transformation matrices \(U_R\) and \(U_S\). The matrices \(\obs_R U_R\) and \(\obs_S U_S\) are then respectively the compressed regular part of the observability matrix and the compressed singular part of the observability matrix. The block diagonal matrix
\begin{equation} \begin{bmatrix} U_R & 0 \\ 0 & U_S \end{bmatrix}, \end{equation}
compresses the entire descriptor system while preserving the sparse matrix structure resulting from the Weierstrass canonical form.
The extended observability matrix
The number of block rows of the observability matrix is equal to the order of the system. As we have demonstrated before, this matrix is large enough to check the observability of the descriptor system, as was the case for regular systems. It is also possible to define the extended observability matrix \(\obs_{0|n-1}\) for some value of \(n\). This matrix is equal to
\begin{equation} \begin{bmatrix} C \mathcal{A}_{n-1}^0 \\ C \mathcal{A}_{n-1}^1 \\ C \mathcal{A}_{n-1}^2 \\ \vdots \\ C \mathcal{A}_{n-1}^{n-1} \\ \end{bmatrix} = \begin{bmatrix} C E^{n-1} \\ C A E^{n-2} \\ C A^2 E^{n-3} \\ \vdots \\ C A^{n-1} E \\ \end{bmatrix}. \end{equation}
For a system with \(q\) outputs, this matrix has \(qn\) rows. When we take \(n\) equal to the order of the descriptor system, the extended observability matrix becomes the observability matrix as defined earlier in this section.
Mind the gap
In the Weierstrass canonical form, we have demonstrated that the observability matrix can be split in two separate matrices, \(\obs_R\) and \(\obs_S\), this is also true for the extended observability matrix. The first matrix is a classical observability matrix of the regular state space model
\begin{equation} \begin{aligned} x[k+1] = & A_R x[k] \\ y[k] = & C_R x[k]. \end{aligned} \end{equation}
This is a state space model representing the causal part of the descriptor system. The second matrix \(\obs_S\) is also an observability matrix of the system
\begin{equation} \begin{aligned} x[k+1] = & N x[k] \\ y[k] = & C_S x[k], \end{aligned} \end{equation}
with the small difference that the order of the rows is reversed, i.e.~the powers of the system matrix \(N\) decrease if the row index increases.
Consider now the extended observability matrix with \(n\) block rows for a descriptor system of order \(m\), this matrix is denoted by \(\obs_{0|n-1}\) and
\begin{equation} \obs_{0|n-1} = \begin{bmatrix} \obs_{R,0|n-1} & \obs_{S,0|n-1} \end{bmatrix} \end{equation}
We will now calculate the number of linear dependent rows of this matrix by analyzing the properties of both matrices \(\obs_{R,0|n-1}\) and \(\obs_{S,0|n-1}\). Denote the number of columns of \(\obs_{R,0|n-1}\) by \(m_r\) and the number of columns of \(\obs_{S,0|n-1}\) as \(m_s\). Because of Theorem \ref{thm:1DR-ch} from Chapter \ref{ch:1DR}, and given that the system is observable we have that the first \(m_r\) rows of \(\obs_{R,0|n-1}\) are linearly independent. The same is true for \(\obs_{S,0|n-1}\), where the last \(m_s\) rows are linearly independent, furthermore, only the last \(p\) rows are non-zero because of the nil potency of the system matrix \(N\). This is visualized in Figure~\ref{fig:1DS-gap}.
In this figure, four extended observability matrices are shown, each matrix has a different order, i.e.~a different number of block rows. The first \(m_r\) block rows are linearly independent, depending on the order of the observability matrix, there are a number of rows which are linearly dependent of the first \(m_r\) block rows. At a certain row-index in the matrix, the rows become linearly independent again, this is due to the rows of the singular part of the system and can be seen by the second blue block in the figure. The region of rows which are all linearly dependent on the first \(m_r\) rows is called the gap. Increasing the order of the extended observability matrix has the effect of increasing the gap in the matrix. In Figure~\ref{fig:1DS-gap-plot} we have plotted the increasing rank of the submatrices obtained by taking the first \(k\) block rows, where \(k\) is shown on the horizontal axis of the plot. From the figure we can see that the rank of the subsequent block matrices increases until 4 and then stabilizes. After adding 10 block rows, the rank of the submatrices increases again.

Figure 1: The effect of increasing the number of rows of the observability matrix of a descriptor system. The blue part in the matrix shows linearly independent rows. The gray part of the matrix contains zeros. The hatched part indicates linearly dependent rows and the orange part can be either dependent or independent. The order of these matrices is equal to the number of block rows and is indicated at the top. When the order increases, the so called ‘gap’ increases as well. The dashed lines indicate linear independent rows in each of the submatrices (obs_R) and (obs_S).
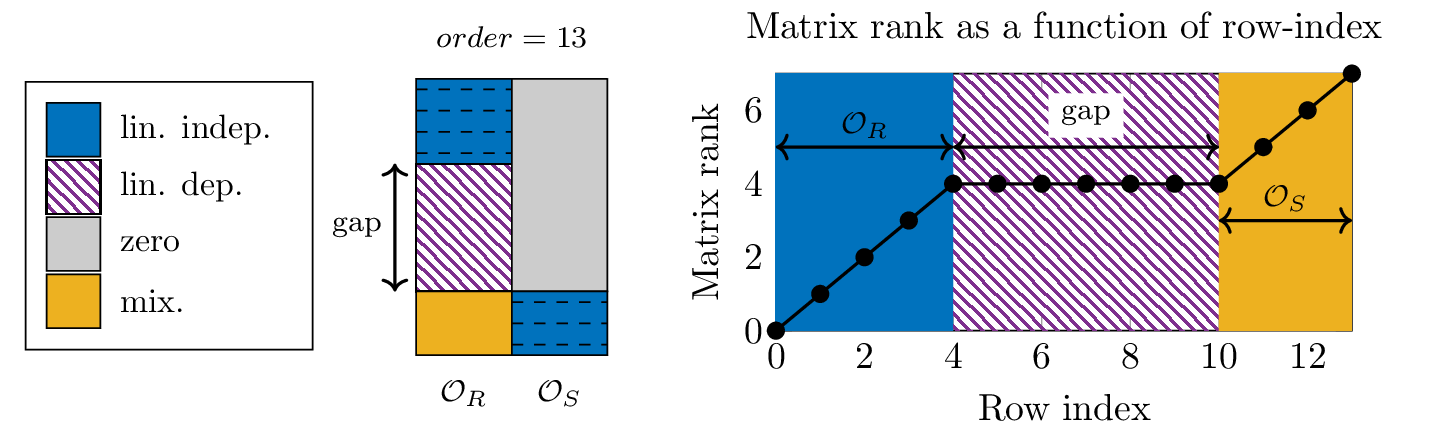
Figure 2: In this figure, we show the increasing rank of the submatrices obtained by taking the first (k) rows of the extended observability matrix. In the left figure we show the sparse structure of the extended observability matrix of order 13. The part indicated by (obs_R) is the regular part of the observability matrix, and the part indicated by (obs_S) is the singular part of the observability matrix. The first 4 rows of the matrix are linearly independent. The next 6 rows are linearly dependent and the last 4 rows are again independent. The gap is the region of rows between row 4 and row 10.
Separating the regular and singular dynamics
An important application of the gap is the ability to separate the causal and non-causal dynamics of the system in the observability matrix. For example, when the system matrices are not put in the WCF, the regular and singular dynamics are not separated in the observability matrix. In order to separate both dynamics we have to identify the first \(m_r\) linearly independent rows and the gap. This can be done by either calculating the rank of the submatrices obtained by taking the first \(k\) block-rows or checking if the current row is linearly independent of the previous rows. In this way we can find:
- the order of the regular part of the system,
- the linearly dependent rows, i.e.~the gap.
After identifying the gap and the number of linearly independent rows in the gap, we can calculate a column compression to separate the regular and singular dynamics.
Popov–Belevitch–Hautus
Similar to the regular system, we can formulate a second condition to verify the observability of descriptor systems. This is done by Popov–Belevitch–Hautus (PBH) test for singular systems.
The state space model from Equation~\eqref{eqn:1S-SS} with \(q\) outputs and a $m$-dimensional state vector, parameterized by the regular, commuting matrix pencil \((A,E)\) and output matrix \(C\), is observable if and only if the \((q+m)\times m\) dimensional matrix
\begin{equation} \begin{bmatrix} A- \lambda E \\ C \end{bmatrix} \end{equation}
has rank \(m\) for all finite, possibly complex values of \(\lambda\) and the matrix
\begin{equation} \begin{bmatrix} E \\ C \end{bmatrix} \end{equation}
has full rank.
This was proven in~\cite{daisingular}. % Theorem 2-3.1.
Controllability
We now shift our attention to the topic of controllability of descriptor systems. As mentioned before, the state sequence of a descriptor system can be split in a regular and a singular part. We first start by describing the state sequence matrix of a descriptor system, followed by a description of the row compression.
State sequence matrix
The state sequence of a descriptor system has been discussed in Section~\ref{sec:1S-state-sequence}. For the descriptor system in Equation~\eqref{eqn:1S-SS} where both system matrices commute, the state sequence matrix is
\begin{equation} X =\begin{bmatrix} \mathcal{A}^0_{m-1}x & \mathcal{A}^1_{m-1} x & \cdots & \mathcal{A}^{m-1}_{m-1} \end{bmatrix}. \end{equation}
When the system is placed in the Weierstrass canonical form, this expression becomes
\begin{equation}\label{eqn:1S-state-sequence} X = \begin{bmatrix} x_{R} & A_Rx_{R} & \cdots & A_R^{m-2}& A_R^{m-1} x_{R} \\ 0 & 0 & \cdots & Nx_S & {x}_{S} \end{bmatrix}. \end{equation}
The state consists of two parts, one part that contains the regular dynamics, running forwards and another that contains the singular dynamics, running backward.
Row compression
To calculate the row compression of the state sequence matrix from Equation~\eqref{eqn:1S-state-sequence} we calculate the row compression of the regular and the singular part separately. This procedure is the same as for the column compression of descriptor system.
Kalman decomposition
A descriptor system can be split in four different components just like in the regular case. We have,
- a system that is controllable and observable,
- a system that is controllable but not observable,
- a system that observable but not controllable,
- and a system which is neither controllable nor observable.
The part of the system that is controllable and observable is the minimal realization of the system. The calculation of the Kalman decomposition follows the same reasoning as in Section~\ref{sec:1DR-kalman} of Chapter~\ref{ch:1DR}.
Modal analysis
The modal analysis follows the same line as the analysis for one-dimensional regular systems, performed in Section~\ref{sec:1d_modal} of Chapter~\ref{ch:1DR}. Consider the descriptor system which is placed in the WCF, as shown in Equation~\eqref{eqn:1S-wcf}. The output of the system over the finite horizon with \(0\leq k \leq n\) is then equal to
\begin{equation} y[k] = C_{R}A_{R}^{k}x_{R}[0] + C_{S}N^{n-k}{x}_{S}[n], \end{equation}
which contains two parts \(y_R[k] = C_{R}A_{R}^{k}x_{R}[0]\) and \(y_S[k] = C_{S}N^{n-k}{x}_{S}[n]\), respectively a regular and a singular part. The modal solutions of the regular part has been analyzed in Section~\ref{sec:1d_modal}. The singular term \(y_S[k]\) is special because the system runs backward and the eigenvalues of \(N\) are all zero because of the nilpotency. Similar to Section~\ref{sec:1d_modal} we introduce the subspace \(\mathcal{M}_p^l\) of the complex vector space \(\complex^{m}\) as
\begin{equation} \mathcal{M}_p^l = \left\lbrace x \in \complex^{m} | N^lx =0 \right\rbrace, \end{equation}
If \(x_\mu[0] \in \mathcal{M}_p^{\mu}\), but \(x_\mu[0] \notin \mathcal{M}_p^{\mu-1}\), we have proven that
\begin{equation}\label{eqn:modes1d-v2} x_{\mu}[k] = \sum_{j=1}^{\mu} \binom{k}{\mu-j}0^{k-\mu+j}N^{\mu-j} x_\mu[0]. \end{equation}
Note that the powers of \(0\) can be simplified as
\begin{equation} 0^q = \begin{cases} 1 & q=0 \\ 0 & q\neq 0 \end{cases}. \end{equation}
Using this relation, we see that all terms in the sum of Equation~\eqref{eqn:modes1d-v2} are zero except when \(j = \mu-k\). In this way we find that
\begin{equation} x_{\mu}[k] = N^{k} x_\mu[0] = \begin{cases} 0 & k = j-\mu \\ 1 & k \neq j-\mu \end{cases}. \end{equation}
The only difference between \(x_\mu[k]\) and \(x_{S}[k]\) is that the latter runs backward. We can thus conclude that each generalized eigenvector of \(N\) corresponds to an eigenmode of the system. The eigenmodes propagate only finitely many samples, starting from the end.
Conclusion
In this chapter we analyzed one-dimensional descriptor systems. The dynamics and properties of a descriptor system are largely determined by the associated matrix pencil, which must be regular in order for the system to be well-posed. To analyze the descriptor system, we looked at two specials forms; the case of the commuting descriptor systems, and the case of the WCF. Our analysis led to the introduction of novel evolution operator, which generalizes the role of the single system matrix of regular one-dimensional state space models. This evolution operator appeared in the theorem of Cayley–Hamilton as well as in the description of observability and controllability.
The use of the evolution operator instead of the explicit calculations in the WCF, i.e.~the classical approach, simplifies most of the results, which also allowed us to spot a small mistake in the existing literature.
In the next chapters we will see that the evolution operators can be introduced to analyze multi-dimensional descriptor systems. Furthermore, we will show that the unique arithmetic properties of this operator leads to a novel realization algorithm, presented in following chapters.