The class of commuting state space models presented in Chapter~\ref{ch:2DR} can be extended to cover Differential Algebraic Equations or descriptor systems. As shown in Chapter~\ref{ch:1DS} these systems are characterized by a causal and non-causal part. In this chapter two-dimensional, and to some extend multi-dimensional, descriptor systems are described.
It has been shown that the commutativity of the system matrices of a multi-dimensional commuting state space model is important for the well-posedness of this class of state space models. We will start by deriving a similar condition for the well-posedness of the class of descriptor systems, where we show that commutativity is no longer directly required. This leads to the introduction of an extension of the Weierstrass canonical form for multi-dimensional commuting descriptor systems.
The Weierstrass canonical form is later used to describe the causal and non-causal solutions of this class of systems. We also introduce the observability and state sequence matrices for this model class and finally derive the modal solution.
The class of descriptor systems
In this chapter the properties of linear autonomous descriptor systems in two dimensions, and to some extend higher dimensional systems, are analyzed. A natural question to ask is \textit{under what condition are these systems well-posed and what is the solution for the state sequence, given specified initial and final conditions?} We demonstrate that, in the same way as in the one-dimensional case, the output of a descriptor system in two dimensions can be decoupled in a causal and non-causal part.
The proposed model class is parameterized by the following model equation
\begin{equation}\label{eqn:DS2D} \begin{aligned} E x[k+1,l] = & A x[k,l] \\ F x[k,l+1] = & B x[k,l] \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
with \(y[k,l] \in \real^q\) and \(x[k,l] \in \real^m\), the output and the state vector of the system respectively. The system matrices, denoted by \(A, B, E\) and \(F\), are elements of \(\real^{m\times m}\) and both matrix pencils \((A,E)\) and \((B,F)\) are regular. The matrices \(E\) and \(F\) are in general non-invertible. If both matrices were invertible, the descriptor system could be transformed to a regular two-dimensional state space model by pre-multiplying both equations with the inverse of these matrices.
As shown in Chapter~\ref{ch:2DR}, not all commuting state space models are well-posed. A necessary and sufficient conditions was that the system matrices must commute. In this chapter we derive a similar condition for this model class and derive a canonical form.
Well-posedness condition
Before we proceed, it is important to establish a notion of what we mean by \textit{well-posed}. A set of equations is well-posed, if and only if, a non-trivial solution exists. In the case of a regular two-dimensional commuting state space model we have shown that both system matrices, must commute with one another. When this is not the case, the state vector at multi-index \([k,l]\) does not exist for all indices \(k \geq 0\) and \(l \geq 0\).
A second condition that we require is that the initial state must be a free parameter of the system. Take for example the two-dimensional system from Equation~\eqref{eqn:ss2d} with system matrices
\begin{equation} A = \begin{bmatrix} 1 & 0\\ 0 & 2 \end{bmatrix}, B = \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}, \end{equation}
both matrices do not commute and
\begin{equation} AB - BA = \begin{bmatrix} 0 & -1 \\ 0 & 0 \end{bmatrix} = L. \end{equation}
However, notice that the matrix \(L\) is not of full rank and the vector \(x[0,0] = [1,0]^{T}\) lies in its right null space. We therefore have that \(ABx[0,0] = BAx[0,0]\) and
\begin{equation} x[k,l] = A^kB^lx[0,0] = BA^kB^{l-1}x[0,0] = \dots = B^lA^kx[0,0], \end{equation}
such that there exists a non-trivial state sequence that satisfies the system equations. In this case, the state vector is not a free parameter because it can only lie in the one-dimensional subspace span by the vector \([1,0]^{T}\).
Describing the well-posedness in general for descriptor systems is further complicated by the non-causal nature of the state sequence. This makes that the initial state is not a free parameter in general, even in the one-dimensional case where the solution is determined by a causal state and a non-causal state. We solved this problem in Chapter~\ref{ch:1DS} by introducing the generalized state vector. A similar approach is followed in this chapter.
The notion of well-posedness we propose includes;
- the collection of the initial and final states are free parameters of the system and
- a consistency condition, that guarantees that the value of the state vector is independent on the path followed while traversing the two-dimensional time series data.
We will demonstrate in this chapter, that both conditions impose certain commutativity constraints between the system matrices, when the system is transformed in a certain basis.
Definition of well-posedness
Based on the example above, we formally define the well-posedness condition for a two-dimensional descriptor system.
The two-dimensional descriptor system from Equation~\eqref{eqn:DS2D} with an \(m\) dimensional state vector, parameterized by an output matrix \(C\), the four system matrices \((E,A,F,B)\) and defined for the multi-index \([k,l]\) with \(0\leq k \leq n_1\) and \(0\leq l \leq n_2\) is well-posed if and only if there exist \(m\) linearly independent solutions for the state sequence.
The definition of well-posedness is a little bit more involved than just stating that the initial state must be a free-parameter of the system. We demonstrated in Chapter~\ref{ch:1DS} that the solution of a descriptor system is not only determined by the initial state but also by its final state. This is why the combination of all possible finale states and the initial states must be linearly independent and it is not sufficient to only look at the number of linear independent initial states. By saying that there must exist \(m\) linearly independent time series for the state vector, we combine the degrees of freedom from picking an appropriate initial state and final state.
Well-posedness theorem for two-dimensional descriptor systems
In this chapter we derive a method and a corresponding theorem to check if a descriptor system is well-posed or not. The presented theorem allows us to calculate the eigenmodes of a given descriptor system. The main theorem that guarantees the well-posedness of a descriptor system is as follows.
The two-dimensional system
\begin{equation}\label{eqn:2Ds-model} \begin{aligned} E x[k+1,l] = & A x[k,l], \\ F x[k,l+1] = & B x[k,l], \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
with \((A,E)\) and \((B,F)\), two regular pencils of size \(m \times m\), is well-posed if and only if there exist square matrices \(P\), \(Q\), and \(U\) of full rank such that the four transformed matrices \(PEQ,PAQ,UFQ\) and \(UBQ\) all pairwise commute.
Proving this theorem consists of two distinct steps.
- If the model is well-posed, i.e.~if \(m\) linearly independent solutions exist we have to show that the model can be transformed according to the theorem.
- If the model is transformed according to the theorem, we have to show that the model is well-posed.
This last step is by far the easiest step to do. We will first show that the two systems
\begin{equation} \begin{aligned} E x[k+1,l] = & A x[k,l], \\ F x[k,l+1] = & B x[k,l], \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
and
\begin{equation} \begin{aligned} PEQ x[k+1,l] = & PAQ x[k,l], \\ UFQ x[k,l+1] = & PBQ x[k,l], \\ y[k,l] = & CQ x[k,l], \end{aligned} \end{equation}
are equivalent, where \(P,Q\) and \(U\) are square matrices of full rank. After this we will show that a solution exists when all four system matrices do commute.
Proving the first implication, \textit{if a solution exists, than the system can be transformed} is the harder part of the analysis, which is the topic of Section \ref{sec:descriptor2d}.
The Weierstrass canonical form
We first define the Weierstrass canonical form for a pair of regular matrix pencils, where all matrices form a commuting family.
Given two regular matrix pencils \((A,E)\) and \((B,F)\) where all four matrix form a commuting family. The Weierstrass canonical form for both pencils is
\begin{equation} E = \begin{bmatrix} \eye & & & \\ & \eye & & \\ & & E_{1} & \\ & & & E_{2} \\ \end{bmatrix}, A = \begin{bmatrix} A_{1}& & & \\ & A_{2} & & \\ & & \eye & \\ & & & \eye \\ \end{bmatrix}, \end{equation}
\begin{equation} F = \begin{bmatrix} \eye & & & \\ & F_{1} & & \\ & & \eye & \\ & & & F_{2} \\ \end{bmatrix}, B = \begin{bmatrix} B_{1}& & & \\ & \eye & & \\ & & B_{2} & \\ & & & \eye \\ \end{bmatrix}, \end{equation}
where
- \(A_1\) and \(B_1\) commute,
- \(A_2\) and \(F_1\) commute,
- \(E_1\) and \(B_2\) commute,
- \(E_2\) and \(F_2\) commute,
and \(E_1\), \(E_2\), \(F_1\) and \(F_2\) are nilpotent matrices.
A simple hypothesis
To demonstrate the complexity and the involved mathematical operations for finding a canonical model representation, we start with a simple hypothesis, namely that \textit{the descriptor system is only well-posed \textbf{if and only if} all four system matrices commute}. This hypothesis reflects my initial approach to this problem and is valid for all regular systems where \(E = F = \eye\). In this case the hypothesis reduces to the condition that both system matrices \(A\) and \(B\) must commute, as the identity matrix commutes with all other square matrices of the same size. In this section we briefly touch upon this hypothesis and demonstrate why this idea is flawed.
Hypothesis: All system matrices do commute
Assume for now that all four system matrices which parameterize the descriptor system from Equation~\eqref{eqn:DS2D} pairwise commute. In this case, the state sequence
\begin{equation}\label{eqn:2S-solution1} x[k,l] = A^kE^{n_1-k}B^{l}F^{n_2-l}x, \end{equation}
with \(0\leq k \leq n_1\) and \(0 \leq l \leq n_2\) satisfies the system equations for every vector \(x\). This can be explicitly verified as
\begin{equation*} Ex[k+1,l] = E(A^{k+1}E^{n_1-k-1}B^{l}F^{n_2-l})x = A(A^{k}E^{n_1-k}B^{l}F^{n_2-l}) x = Ax[k,l], \end{equation*}
and, similarly
\begin{equation*} Fx[k,l+1] = F(A^{k}E^{n_1-k}B^{l+1}F^{n_2-l-1})x = B(A^{k}E^{n_1-k}B^{l}F^{n_2-l}) x = Bx[k,l]. \end{equation*}
We can further simplify the Equation~\eqref{eqn:2S-solution1} by using the evolution operator defined in Chapter~\ref{ch:1DS}
\begin{equation} \mathcal{A}^k_{n_1} = A^kE^{n_1-k},~\mathcal{B}^l_{n_2} = B^lE^{n_2-l}. \end{equation}
Using this notation, we can rewrite Equation~\eqref{eqn:2S-solution1} as
\begin{equation}\label{eqn:2S-sate-sequence-hypo} x[k,l] = \mathcal{A}^k_{n_1} \mathcal{B}^l_{n_2} x. \end{equation}
From this equation it is not trivial to calculate an explicit solution for the state vector. However, we will show that it is possible to determine a solution as an explicit function of the eigenvalues and generalized eigenvectors of both matrix pencils \((A,E)\) and \((B,F)\). This is done in Section~\ref{sec:2S-modal}.
This small example proves that if all system matrices commute, the state space model is well-posed and the state sequence is described by Equation \eqref{eqn:2S-sate-sequence-hypo}. The result is summarized in the following Lemma.
If all four system matrices commute the descriptor system of Equation \eqref{eqn:2Ds-model} is well-posed and the solution for the state vector is
\begin{equation} x[k,l] = A^kE^{n_1-k}B^{l}F^{n_2-l}x, \end{equation}
for \(0\leq k \leq n_1\) and \(0\leq l \leq n_2\) and for any vector \(x\).
% Lemma~\cite{lem:2DS-implication-one} proofs the first implication of the well-posedness theorem.
% ** The Weierstrass canonical form
Assume for now that the presented hypothesis is true, which is unfortunately not the case as we will show in the next section. Because all four system matrices form a commuting family, there exists a basis \(U\) in which every system matrix is a block diagonal matrix and every block has a constant diagonal and is upper triangular. In this basis the four system matrices are equal to
\begin{equation} X = \begin{bmatrix} X_1 & 0 & \cdots & 0\\ 0 & X_2 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & X_n \\ \end{bmatrix}, \end{equation}
where \(X\) can be replaced by \(A, B, E\) or \(F\). Note that the order of the blocks \(X_i\) can be changed by using row and column permutations. We can now classify 4 different cases based on the eigenvalues of the block on the diagonals of the 4 system matrices. For some \(i\) we have:
- \(E_i\) and \(F_i\) have non-zero eigenvalues and can be inverted or,
- \(E_i\) has a zero eigenvalue and \(F_i\) has a non-zero eigen value. Due to the regularity of the matrix pencil \((A,E)\) the matrix \(A_i\) can be inverted and \(F_i\) can be inverted or,
- \(F_i\) has a zero eigenvalue and \(E_i\) has a non-zero eigen value. Due to the regularity of the matrix pencil \((B,F)\) the matrix \(B_i\) can be inverted and \(E_i\) can be inverted or,
- both \(E_i\) and \(F_i\) have a zero eigen-value and \(A_i\) and \(B_i\) can be inverted.
Using these four cases, it is possible to transform the system matrices in to the Weierstrass canonical form defined in Definition~\ref{def:2DS-WCF}.
Counter example
\renewcommand{\Eone}{\begin{bmatrix} 1 & 1 \\ 3 & 3 \end{bmatrix}} \renewcommand{\Aone}{\begin{bmatrix} 1 & 5 \\ 3 & 11 \end{bmatrix}} \renewcommand{\Etwo}{\begin{bmatrix} 0 & 6 \\ 0 & 8 \end{bmatrix}} \renewcommand{\Atwo}{\begin{bmatrix} 15 & 39 \\ 21 & 53 \end{bmatrix}} \renewcommand{\C}{\begin{bmatrix} 1 & 1 \end{bmatrix}}
From our first investigation it looks like commutativity of the four system matrices is a necessary condition for the existence of a state sequence. However, we can easily find a counter example where not all four matrices commute but, where the system is nevertheless well-posed.
Consider the proposed descriptor system
\begin{equation} \begin{aligned} \Eone x[k+1,l] = & \Aone x[k,l], \\ \Etwo x[k,l+1] = & \Atwo x[k,l], \\ y[k,l] = & \C x[k,l], \end{aligned} \end{equation}
It can be verified that non of the system matrices pairwise commute with one another. \textit{Is this system well-posed or not?} In this form, this question is non-trivial.
A standard technique to find a solution, is to apply a change of basis to the existing problem, thereby simplifying the equations. For regular two-dimensional state space models, this basis is the eigenbasis of a system matrix. In this case we can work with the Weierstrass canonical form, and apply this transformation to the first dynamic equation of the descriptor system. The WCF of \((A,E)\) is equal to
\begin{equation} (P_1AQ_1,P_1EQ_1) = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix}, \end{equation}
with
\begin{equation} P_1 = \frac{1}{4} \begin{bmatrix} -8 & 4 \\ 3 & -1 \end{bmatrix}, Q_1 = \begin{bmatrix} 1& -1 \\ 0 & 1 \end{bmatrix}. \end{equation}
To apply this transformation to the descriptor system in our example, we multiply the first dynamic equation with \(P_1\) from the left and apply a change of basis such that \(z=Q_1^{-1}x\). Both operations are allowed, as long as both transformations are of full rank and the change of basis is also applied to the second dynamic equation. The transformed descriptor system is than equal to
\renewcommand{\Eone}{\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}} \renewcommand{\Aone}{\begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix}} \renewcommand{\Etwo}{\begin{bmatrix} 0 & 6 \\ 0 & 8 \end{bmatrix}} \renewcommand{\Atwo}{\begin{bmatrix} 15 & 24 \\ 21 & 32 \end{bmatrix}} \renewcommand{\C}{\begin{bmatrix} 1 & 0 \end{bmatrix}}
\begin{equation} \begin{aligned} \Eone z[k+1,l] = & \Aone z[k,l], \\ \Etwo z[k,l+1] = & \Atwo z[k,l], \\ y[k,l] = & \C z[k,l]. \end{aligned} \end{equation}
This new, but equivalent, descriptor system does now have a more tractable form, however the matrices in the second dynamic equation do still not commute.
To fix this, we can put the second equation in a WCF, the problem with this operation is that it would apply a change of basis to the state vector, which would destroy the canonical form of the first system equation, negating our progress so far. The only degree of freedom that we have left is to multiply the second dynamic equation from the left by some non-singular matrix. In this case we multiply the second dynamic equation by
\begin{equation} P_2 = \frac{1}{6} \begin{bmatrix} -8 & 6 \\ 21 & -15 \end{bmatrix} \end{equation}
The final descriptor system is than equal to
\renewcommand{\Eone}{\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}} \renewcommand{\Aone}{\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}} \renewcommand{\Etwo}{\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}} \renewcommand{\Atwo}{\begin{bmatrix} 1 & 0 \\ 0 & 4 \end{bmatrix}} \renewcommand{\C}{\begin{bmatrix} 1 & 0 \end{bmatrix}}
\begin{equation} \begin{aligned} \Eone z[k+1,l] = & \Aone z[k,l], \\ \Etwo z[k+1,l] = & \Atwo z[k,l], \\ y[k,l] = & \C z[k,l]. \end{aligned} \end{equation}
In this form, all four system matrices do commute and it is clear that the system is non-observable because the output matrix has a zero and all matrices are put in a diagonal form. The observable part of the system is
\begin{equation}\label{eqn:example2ddssimple} \begin{aligned} z[k+1,l] = & z[k,l], \\ 0 z[k,l+1] = & z[k,l], \\ y[k,l] = & z[k,l]. \end{aligned} \end{equation}
This is an enormous simplification from the original problem.
To solve this equation, we will restrict the state sequence for \(0 \leq k \leq 4\) and \(0 \leq l \leq 4\). The first dynamic equation states that the state vector is constant along the \(k\) index such that
\begin{equation} z[k,l] = c[l], \end{equation}
for some values of \(c[l]\). Plugging in these values in the second system equation for the various values of \(l\) we find,
\begin{equation} \begin{aligned} 0 c[1] = c[0], \\ 0 c[2] = c[1], \\ 0 c[3] = c[2], \\ 0 c[4] = c[3]. \\ \end{aligned} \end{equation}
The only valid solution to this problem is when \(c[0]=c[1]=c[2]=c[3]=0\) and \(c[4]\) is a free parameter. The modal solution to this problem is than equal to
\begin{equation} y[k,l] = z[k,l] = 0^{4-k}c[4] \end{equation}
The data matrix \(Z\) containing the state such that \(Z[k,l] = z[k,l]\) is than equal to
\begin{equation} Z = \begin{bmatrix} 0 & 0 & 0 & 0 & c[4] \\ 0 & 0 & 0 & 0 & c[4] \\ 0 & 0 & 0 & 0 & c[4] \\ 0 & 0 & 0 & 0 & c[4] \\ \end{bmatrix} \end{equation}
The entire state sequence has one degree of freedom, which is equal to the number of state elements of the observable part of the system. The solution of the non-observable state can be found in a similar way. According to our definition, the state space model from Equation~\eqref{eqn:example2ddssimple} is well-posed, because we can find two linearly independent state sequences which satisfy the dynamic equations, one observable and one non-observable, from which only the observable solution has been calculated.
This initial example demonstrates all challenges associated to the analysis of descriptor systems. We have shown that the system matrices do not per se have to commute in order for the system to be well-posed. The fundamental reason for this is the fact that commutation of matrices is not invariant under the left and right multiplication with a matrix.
Two square matrices can always be transformed via a left and right matrix multiplication such that both matrices commute. An example of such a transformation is the Weierstrass canonical form of a matrix pencil, or the standard form of a matrix pencils.
The permitted operation on a two-dimensional descriptor system are summarized in the following lemma.
Given 3 square matrices \(P, Q\) and \(U\) of full rank. The descriptor system
\begin{equation} \begin{aligned} PEQ x[k+1,l] = & PAQ x[k,l] \\ UFQ x[k,l+1] = & PBQ x[k,l] \\ y[k,l] = & CQ x[k,l], \end{aligned} \end{equation}
is equivalent to the system in Equation~\eqref{eqn:DS2D}.
Combining both results from Lemma~\ref{lem:2DS-implication-one} and Lemma~\ref{lem:2DS-manipulations} proves the first part of the implication presented in Theorem~\ref{thm:2S-all-commuting}. This is summarized in the following lemma.
The two-dimensional system
\begin{equation} \begin{aligned} E x[k+1,l] = & A x[k,l], \\ F x[k,l+1] = & B x[k,l], \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
with \((A,E)\) and \((B,F)\), two regular pencils of size \(m \times m\), is well-posed \textbf{if} there exist square matrices \(P\), \(Q\), and \(U\) of full rank such that the four transformed matrices \(PEQ,PAQ,UFQ\) and \(UBQ\) all pairwise commute.
In the next part of this chapter we also prove the second implication, that is, if the system is well-posed, i.e.~if \(m\) linearly independent state sequences exists, we show that the system can be transformed to the canonical form.
A well-posed system has a canonical form
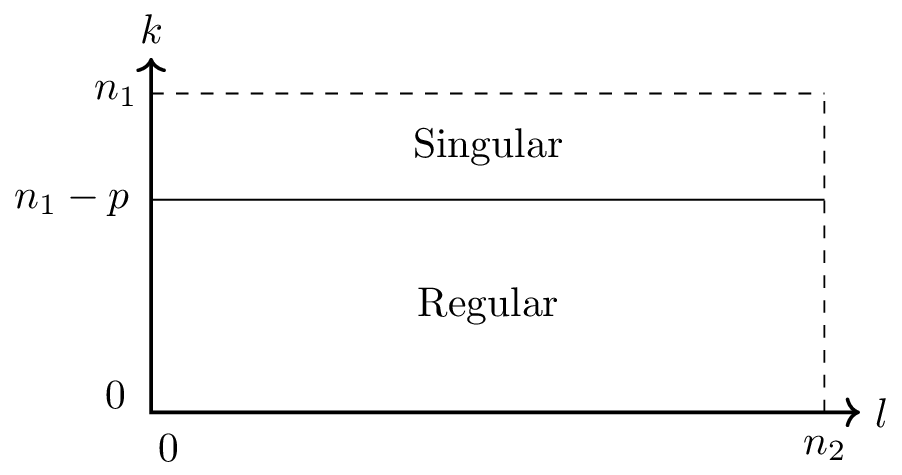
Figure 1: Partitioning of the state sequence of size (n_1times n_2). For small values of (k), the state sequence is only determined by the causal dynamics of the system. For larger values of (k) the non-causal dynamics start to affect the state.
Assume that the descriptor system from Equation~\eqref{eqn:DS2D} is well-posed. According to the definition, a set of \(m\) linearly independent state sequences exist on the grid \(0\leq k \leq n_1\) and \(0\leq l \leq n_2\). We assume that the first model equation is placed in the WCF, this can always be assumed without loss of generality, as a the descriptor system can be transformed when this would not be the case. We have
\begin{equation}\label{eqn:2DS-proof-one} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}, \end{equation}
where \(x^R \in \real^{m_R}\) and \(x^S \in \real^{m_S}\). The solution to this equation is
\begin{equation} \begin{aligned} x^R[k,l] = & A_r^k x^R[0,l] \\ x^S[k,l] = & N^{n_1-k} x^S[n_1,l] \end{aligned} \end{equation}
for some \(0\leq l \leq n_2\). In this basis the second state update equation is
\begin{equation}\label{eqn:2DS-proof-two} \begin{bmatrix} F_{1,1} & F_{1,2} \\ F_{2,1} & F_{2,2} \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^S[k,l+1] \end{bmatrix} = \begin{bmatrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{equation}
Notice that Equation~\eqref{eqn:2DS-proof-one} partitions the state sequence in two parts, as shown in Figure~\ref{fig:2DS-partition-one}. For small values of \(k\), the singular part of the dynamics becomes zero. In this region of the state sequence, Equation~\eqref{eqn:2DS-proof-two} simplifies as
\begin{equation} \begin{bmatrix} F_{1,1} \\ F_{2,1} \end{bmatrix} x^R[k,l+1] = \begin{bmatrix} B_{1,1} \\ B_{2,1} \end{bmatrix} x^R[k,l]. \end{equation}
Which can be transformed to
\begin{equation} \begin{bmatrix} F_{1,1} & -B_{1,1} \\ F_{2,1} & -B_{2,1} \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^R[k,l] \end{bmatrix} = 0. \end{equation}
In order for the state to be a free parameter, this expression must have a solution for any value of the initial state, which implies that the matrix in the left hand side, must be rank deficient and has an $m_r$-dimensional right null space. Note that the size of the matrix is \(m \times 2m_r\), from which we can conclude that the rank of the matrix is at most \(m_r\). It follows that there exists a transformation with the full matrix \(U\) such that
\begin{equation} U \begin{bmatrix} F_{1,1} & -B_{1,1} \\ F_{2,1} & -B_{2,1} \end{bmatrix} = \begin{bmatrix} F’_{1,1} & -B’_{1,1} \\ 0 & 0 \end{bmatrix} \end{equation}
This is essentially a row compression, which can be calculated by using the SVD. We now apply this row compression to Equation~\ref{eqn:2DS-proof-two} and get
\begin{equation}\label{eqn:2DS-proof-three} \begin{bmatrix} F_{1,1}’ & F_{1,2}’ \\ 0 & F_{2,2}' \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^S[k,l+1] \end{bmatrix} = \begin{bmatrix} B_{1,1}’ & B_{1,2}’ \\ 0 & B_{2,2}' \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{equation}
We will now take a closer look at the second region of the state vector, depicted in Figure~\ref{fig:2DS-partition-one}, in which the state sequence is determined by the regular and singular dynamics of the first state update equation. Without loss of generality we can assume that \(x^R[k,l]\) is zero, this is because the state is an independent variable. In this case, Equation~\eqref{eqn:2DS-proof-three} simplifies as
\begin{equation}\label{eqn:2DS-proof-four} \begin{bmatrix} F_{1,2}’ \\ F_{2,2}' \end{bmatrix} x^S[k,l+1] = \begin{bmatrix} B_{1,2}’ \\ B_{2,2}' \end{bmatrix} x^S[k,l]. \end{equation}
which is rewritten as
\begin{equation}\label{eqn:2DS-proof-five} \begin{bmatrix} F_{1,2}’ & -B_{1,2}’ \\ F_{2,2}’ & -B_{2,2}' \end{bmatrix} \begin{bmatrix} x^S[k,l+1] \\ x^S[k,l] \end{bmatrix} = 0. \end{equation}
The matrix in the left hand side has size \(m \times 2m_s\) and the right null space is at least $m_s$-dimensional from which it follows that the matrix has at most rank \(m_s\). We will now show that the matrix in the left hand side has exactly rank \(m_s\).
Part of the model definition was the assumption that the matrix \((B,F)\) is regular. This implies that \((B_{2,2}’,F_{2,2}’)\) is also regular as it is a block diagonal element of the matrix pencil \((UB,UF)\) and therefor we have that the matrix
\begin{equation} \begin{bmatrix} F_{2,2}’ & -B_{2,2}' \end{bmatrix} \in \real^{m_s \times 2 m_s} \end{equation}
has full rank, i.e.~has rank \(m_s\). This in turn proves that the matrix
\begin{equation} \begin{bmatrix} F_{1,2}’ & -B_{1,2}’ \\ F_{2,2}’ & -B_{2,2}' \end{bmatrix} \end{equation}
has exactly rank \(m_s\) and that the last \(m_s\) rows are linearly independent. Because of this, there exists a transformation matrix \(V\) such that
\begin{equation} \begin{bmatrix} V_{1,1} & V_{1,2} \\ 0 & V_{2,2} \end{bmatrix} \begin{bmatrix} F_{1,2}’ & -B_{1,2}’ \\ F_{2,2}’ & -B_{2,2}' \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ F_{2,2}’’ & -B_{2,2}’' \end{bmatrix}. \end{equation}
Applying this transformation to the second model equation results in
\begin{equation}\label{eqn:2DS-proof-six} \begin{bmatrix} F_{1,1}’’ & 0 \\ 0 & F_{2,2}’' \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^S[k,l+1] \end{bmatrix} = \begin{bmatrix} B_{1,1}’’ & 0 \\ 0 & B_{2,2}’' \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{equation}
The final model given by
\begin{equation} \begin{aligned} E x[k+1,l] = & A x[k,l], \\ VUF x[k,l+1] = & VUB x[k,l], \\ y[k,l] = & CQ x[k,l], \end{aligned} \end{equation}
is transformed in a way such that
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} F_{1} & 0 \\ 0 & F_{2} \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B_1 & 0 \\ 0 & B_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
In this basis, the state vector consists of two decoupled parts denoted by \(x^R\) and \(x^S\), which are the solution of
\begin{equation} \begin{array}{c|c} \begin{aligned} x^R[k+1,l] = & A_r x^R[k,l] \\ F_1 x^R[k,l+1] = & B_1 x^R[k,l] \\ y_R[k,l] = & C_R x^R[k,l] \end{aligned} & \begin{aligned} Nx^S[k+1,l] = & x^S[k,l] \\ F_2 x^S[k,l+1] = & B_2 x^S[k,l] \\ y_S[k,l] = & C_S x^S[k,l]. \end{aligned} \end{array} \end{equation}
With our analysis we have proven that the state vector of a well-posed system can be split in two parts namely \(x^R\) and \(x^S\). Each part of the state vector is governed by a simplified version of a descriptor system, we call these systems semi-descriptor systems as one dynamic equation is governed by a matrix pencil and the second equation is governed by a single system matrix.
The result of this section is summarized in the following lemma.
For every well-posed two-dimensional descriptor system of there exist 3 square matrices of full rank, \(P,Q\) and \(U\) such that
\begin{equation} \begin{aligned} PEQ x[k+1,l] = & PAQ x[k,l] \\ UFQ x[k,l+1] = & UBQ x[k,l] \\ y[k,l] = & CQ x[k,l], \end{aligned} \end{equation}
has the form
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} F_{1} & 0 \\ 0 & F_{2} \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B_1 & 0 \\ 0 & B_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
In the next section we apply the same analysis as before to the two semi-descriptor systems to obtain a canonical form for two-dimensional descriptor systems.
Semi-descriptor system of the first form
Consider the semi-descriptor system
\begin{equation}\label{eqn:semidescriptor-one} \begin{aligned} E x[k+1,l] = & A x[k,l] \\ x[k,l+1] = & B x[k,l] \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
where \((A,E)\) is a regular matrix pencil. We have just proven that this model can be transformed to
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} F_1 & 0 \\ 0 & F_2 \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B_1 & 0 \\ 0 & B_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
Note that the matrix
\begin{equation} F = \begin{bmatrix} F_1 & 0 \\ 0 & F_2 \end{bmatrix} \end{equation}
has full rank and can be inverted. When multiplying the second dynamic equation by the inverse of \(F\) we get
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} \eye & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B’_1 & 0 \\ 0 & B’_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
The solution to this equation is
\begin{equation} \begin{aligned} x^R[k,l] = & A_r^kB_1’^l x^R[0,l] \\ x^S[k,l] = & N^{n_1-k}B_2’^l x^S[n_1,0]. \end{aligned} \end{equation}
Which is only well-defined when the matrices \(A_r\) and \(B_1’\) pairwise commute and \(N\) and \(B_2’\) pairwise commute.
The well-posed system from Equation~\eqref{eqn:semidescriptor-one} can be transformed to
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} \eye & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B’_1 & 0 \\ 0 & B’_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
Where \(A_r\) and \(B_1’\) pairwise commute and \(N\) and \(B_2’\) pairwise commute.
Semi-descriptor system of the second form
A second special form of the descriptor system is
\begin{equation}\label{eqn:semidescriptor-two} \begin{matrix} Ex[k+1,l] = & A x[k,l] \\ Fx[k,l+1] = & x[k,l] \\ y[k,l] = & C x[k,l], \end{matrix} \end{equation}
We assume that the first equation has been placed in the Weierstrass canonical form. When the system is well-posed we have shown that the system can be transformed to
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} F_1 & 0 \\ 0 & F_2 \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} B_1 & 0 \\ 0 & B_2 \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
With the same reasoning as before, both matrices \(B_1\) and \(B_2\) are of full rank and the system can be transformed to
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} F’_1 & 0 \\ 0 & F’_2 \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^S[k,l+1] \end{bmatrix} = & \begin{bmatrix} \eye & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
The solution to this equation is
\begin{equation} \begin{aligned} x^R[k,l] = & A_r^kF_1’^{n_2-l} x^R[0,n_2] \\ x^S[k,l] = & N^{n_1-k}F_2’^{n_2-l} x^S[n_1,n_2]. \end{aligned} \end{equation}
This result is summarized in the following lemma.
The well-posed system from Equation~\eqref{eqn:semidescriptor-two} can be transformed to
\begin{equation} \begin{aligned} \begin{bmatrix} \eye & 0 \\ 0 & N \end{bmatrix} \begin{bmatrix} x^R[k+1,l] \\ x^S[k+1,l] \end{bmatrix} = & \begin{bmatrix} A_r & 0 \\ 0 & \eye \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ \begin{bmatrix} B’_1 & 0 \\ 0 & B’_2 \end{bmatrix} \begin{bmatrix} x^R[k,l+1] \\ x^S[k,l+1] \end{bmatrix} = & \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix} \\ y[k,l] = & \begin{bmatrix} C_R & C_S \end{bmatrix} \begin{bmatrix} x^R[k,l] \\ x^S[k,l] \end{bmatrix}. \end{aligned} \end{equation}
Where \(A_r\) and \(B_1’\) pairwise commute and \(N\) and \(B_2’\) pairwise commute.
The Weierstrass canonical form for two-dimensional descriptor systems
By combining the results formulated in Lemmas \ref{lem:2DS-lem-one}, \ref{lem:2DS-lem-two} and \ref{lem:2DS-lem-three} we have proven that the a well-posed descriptor system can be placed in the Weierstrass canonical form presented in Definition~\ref{def:2DS-WCF}. In this basis, all four system matrices commute, which proofs the second implication of Theorem~\ref{thm:2S-all-commuting}.
The dynamics of the state vector are described by four sub-systems, which are listed in Table~\ref{tbl:overview-of-partial-moddels}. When the descriptor system is placed in the WCF, the dynamic equations can be written as
\begin{equation}\label{eqn:WCF2d} \begin{aligned} \begin{bmatrix} x^{RR}[k+1,l] \\ x^{RS}[k+1,l] \\ x^{SR}[k-1,l] \\ x^{SS}[k-1,l] \end{bmatrix} = &\begin{bmatrix} A_{1} & & & \\ & A_{2} & & \\ & & E_{1} & \\ & & & E_{2} \\ \end{bmatrix} \begin{bmatrix} x^{RR}[k,l] \\ x^{RS}[k,l] \\ x^{SR}[k,l] \\ x^{SS}[k,l] \end{bmatrix} \\ \begin{bmatrix} x^{RR}[k,l+1] \\ x^{RS}[k,l-1] \\ x^{SR}[k,l+1] \\ x^{SS}[k,l-1] \end{bmatrix} = &\begin{bmatrix} B_{1} & & & \\ & F_1 & & \\ & & B_{2} & \\ & & & F_{2} \\ \end{bmatrix} \begin{bmatrix} x^{RR}[k,l] \\ x^{RS}[k,l] \\ x^{RR}[k,l] \\ x^{RR}[k,l] \end{bmatrix} \\ y[k,l] = &\begin{bmatrix} C_{RR} & C_{RS} & C_{SR} & C_{SS} \end{bmatrix} \begin{bmatrix} x^{RR}[k,l] \\ x^{RS}[k,l] \\ x^{RR}[k,l] \\ x^{RR}[k,l] \end{bmatrix}. \end{aligned} \end{equation}
The solution for the state vector is than
\begin{equation}\label{eqn:states_expression} \begin{aligned} x^{RR}[k,l] = & A_{1}^kB_{1}^lx^{RR}[0,0] \\ x^{RS}[k,l] = & A_{2}^kF_{1}^{n_2-l}x^{RS}[0,n_2] \\ x^{SR}[k,l] = & E_{1}^{n_1-k}B_{2}^lx^{SR}[n_1,0] \\ x^{SS}[k,l] = & E_{2}^{n_1-k}F_{2}^{n_2-l}x^{SS}[n_1,n_2] \\ \end{aligned} \end{equation}
and the output is
\begin{equation} y[k,l] = C_{RR}x^{RR}[k,l] + C_{RS}x^{RS}[k,l] + C_{SR}x^{SR}[k,l] + C_{SS}x^{SS}[k,l]. \end{equation}
The Weierstrass canonical form partitions the state vector in 4 regions, a regular-regular part, a regular- singular part, a singular-regular part and a singular-singular part. These four regions are shown in Figure~\ref{fig:2S-1}.
\begin{table}t] \caption[Sub-systems of a two-dimensional commuting descriptor system in the canonical form.]{ Sub-systems of a two-dimensional commuting descriptor system in the canonical form. } \label{tbl:overview-of-partial-moddels} \centering \begin{tabular}{c|cc} & Regular & Singular \\ \midrule \rotatebox[origin=c]{90}{Regular} & $\begin{array} {r} \\ x[k+1,l] = A_1x[k,l] \\ x[k,l+1] = B_1x[k,l] \\ y[k,l] = C_{RR}x[k,l] \end{array}$ & $\begin{array} {r} \\ x[k+1,l] = A_2x[k,l] \\ F_1x[k,l+1] = x[k,l] \\ y[k,l] = C_{RS}x[k,l] \end{array}$ \\ \rotatebox[origin=c]{90}{Singular} & $\begin{array} {r} \\ E_1x[k+1,l] = x[k,l] \\ x[k,l+1] = B_2x[k,l] \\ y[k,l] = C_{SR}x[k,l] \end{array}$ & $\begin{array} {r} \\ E_2x[k+1,l] = x[k,l] \\ F_2x[k,l+1] = x[k,l] \\ y[k,l] = C_{SS}x[k,l] \end{array}$ \\ \bottomrule \end{tabular} \end{table}
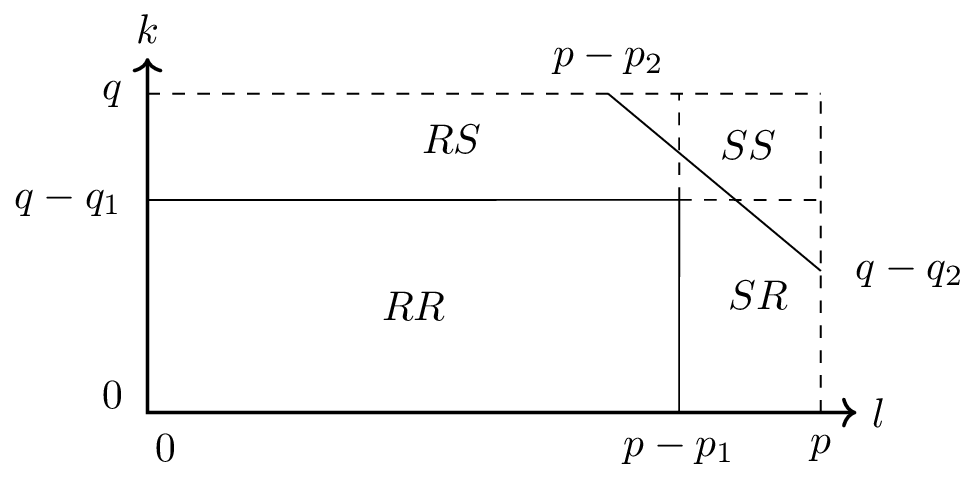
Figure 2: Schematic overview of the regular and singular parts of the state vector on a two-dimensional grid, with the multi-index (0leq k leq m) and (0leq l leq n). The output of the system only depends on the regular part of the state space model for small values of (k) and (l). The singular state of a descriptor system can be associated to a dynamic running backward. For a two-dimensional system descriptor system, we can classify the state in 4 different regions, based on the direction of propagation. The part of the state that runs forward in both indices (k) and (l) is indicated by the region (RR) (regular-regular). The part of the state that runs backward in the dimension indicated by (k) and forward in the dimension indicated by (l) is denoted by (SR) (singular-regular). Two more regions can be identified, the state running forward in (k) and backward is (l), indicated with (SR) (singular-regular) and finally a region where the state runs backward in both (k) and (l). The singular part of the descriptor system is associated with two nilpotent matrices, one for each dimension of the data set. The nilpotency index can be read from the figure, and is indicated by (p_i) and (q_i). These indices form the boundary between the 4 regions in the time series data. }
Cayley–Hamilton for two-dimensional descriptor systems
The Weierstrass canonical form
The existence of a canonical form for commuting descriptor systems allows us to generalize the theorem of Cayley–Hamilton for descriptor systems. This in turn, will be used to derive an expression for the difference equation.
Given the well-posed descriptor system with system matrices \(A,B,E\) and \(F\) all elements of \(\complex^{m\times m}\), forming two regular pencils \((A,E)\) and \((B,F)\). When the system matrices are placed in the canonical form, there exists a non-trivial set of coefficients \(\alpha_{i,j}\) such that
\begin{equation} 0 = \sum_{i=0}^k\sum_{j=0}^{m-k} \alpha_{i,j} A^iE^{m-i}B^{j}F^{m-j}, \end{equation}
for all values of \(0\leq k\leq m\).
Consider the well-posed descriptor system with system matrices \(A,B,E\) and \(F\) all elements of \(\complex^{m\times m}\), forming two regular pencils \((A,E)\) and \((B,F)\). We assume that the four system matrices are placed in there canonical form. As such, these matrices can be written as
\begin{equation} E = \begin{bmatrix} \eye & & & \\ & \eye & & \\ & & E_{1} & \\ & & & E_{2} \\ \end{bmatrix}, A = \begin{bmatrix} A_{1}& & & \\ & A_{2} & & \\ & & \eye & \\ & & & \eye \\ \end{bmatrix}, \end{equation}
\begin{equation} F = \begin{bmatrix} \eye & & & \\ & F_{1} & & \\ & & \eye & \\ & & & F_{2} \\ \end{bmatrix}, B = \begin{bmatrix} B_{1}& & & \\ & \eye & & \\ & & B_{2} & \\ & & & \eye \\ \end{bmatrix}. \end{equation}
All matrices \(E_1,E_2,F_1\) and \(F_2\) are nilpotent. The sizes of the sub-matrices are
- \(A_1\) and \(B_1\) have size \(m_1 \times m_1\),
- \(A_2\) and \(F_1\) have size \(m_2 \times m_2\),
- \(E_1\) and \(B_2\) have size \(m_3 \times m_3\),
- \(E_2\) and \(F_2\) have size \(m_4 \times m_4\).
We also have that \(m_1+m_2+m_3+m_4 = m\).
Consider the pair of commuting matrices \(A_1\) and \(B_1\). According to the regular theorem of Cayley–Hamilton for commuting matrices, there exists a non-trivial set of coefficients \(\alpha_{i,j}\) such that
\begin{equation} 0 = \sum_{i=0}^l\sum_{j=0}^{m_1-l} \alpha_{i,j} A_1^iB_1^{j}, \end{equation}
for all values of \(0\leq l \leq m_1\). We will now proof that
\begin{equation} 0 = \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A^iE^{m-i}B^{j}F^{m-j}. \end{equation}
By using the structure of the four system matrices, we can rewrite this formula as
\begin{equation} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} \begin{bmatrix} A_1^iB_1^j & 0 & 0 & 0 \\ 0 & A_2^iF_1^{m-j} & 0 & 0 \\ 0 & 0 & E_1^{m-i}B_2^{j} & 0 \\ 0 & 0 & 0 & E_2^{m-i}F_2^{m-j} \\ \end{bmatrix}. \end{equation}
This expression is zero if and only if all four equations
\begin{equation}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A_1^iB_1^j,\label{eqn:2DS-proof-1}\end{equation}
\begin{equation}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A_2^iF_1^{m-j},\label{eqn:2DS-proof-2}\end{equation}
\begin{equation}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_1^{m-i}B_2^{j},\label{eqn:2DS-proof-3}\end{equation}
\begin{equation}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_2^{m-i}F_2^{m-j}, \label{eqn:2DS-proof-4}\end{equation}
are simultaneously equal to zero. As per construction, the first equation is identically zero. We can rewrite the second equation as
\begin{equation} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A_2^iF_1^{m-j} = F_1^{m-(m_1-l)} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A_2^iF_1^{(m_1-l)-j}. \end{equation}
Because \(l\) satisfies \(0\leq l \leq m_1\) and all \(m_i\geq 0\), we have that
\begin{equation} m-(m_1-l) = m_2 + m_3 + m_4 + l \geq m_2, \end{equation}
Because the nilpotency index of a matrix is always smaller than the number of columns/rows of that matrix we have that \(F_1^{m-(m_1-l)}\) is equal to zero. Which proofs that
\begin{equation} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A_2^iF_1^{m-j} = 0 \end{equation}
To proof that Equations~\eqref{eqn:2DS-proof-3} and~\eqref{eqn:2DS-proof-4} are zero we follow the exact same reasoning. Such that
\begin{equation}\label{eqn:2DS-eqn-proof-3} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_1^{m-i}B_2^{m-j} = E_1^{m-l}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_1^{l-i}B_2^{j} = 0 \end{equation}
Similar as before we have that
\begin{equation} m-l = (m_1-l)+m_2+m_3+m_4 \geq m_3. \end{equation}
It follows that \(E_1^{m-l}\) is equal to zero such that~\eqref{eqn:2DS-eqn-proof-3} is zero. To finalize this proof, Equation~\eqref{eqn:2DS-proof-4} is rewritten as
\begin{equation} \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_2^{m-i}F_2^{m-j} = E_2^{m-l}F_2^{m-m_1+l}\sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} E_2^{l-i}F_2^{m_1-l-j} \end{equation}
which is also zero.
So far we have restricted \(l\) to be smaller than \(m_1\). Consider a variable \(l\leq k\leq m\). We define a new set of coefficients as
\begin{equation} \beta_{i,j} = \begin{cases} \alpha_{i,j} & \text{for}~i \leq l~\text{and}~j \leq m_1-l, \\ 0 & \text{for}~i > l~\text{or}~j > m_1-l. \end{cases} \end{equation}
We now have
\begin{equation} \sum_{i=0}^k\sum_{j=0}^{m_1-k}\beta_{i,j} A^iE^{m-i}B^{j}F^{m-j} = \sum_{i=0}^l\sum_{j=0}^{m_1-l}\alpha_{i,j} A^iE^{m-i}B^{j}F^{m-j} = 0, \end{equation}
for some value \(0\leq k \leq m\), which proofs Theorem~\ref{thm:2S-CH}.
General case
Given the well-posed descriptor system with system matrices \(A,B,E\) and \(F\) all elements of \(\complex^{m \times m}\), forming two regular pencils \((A,E)\) and \((B,F)\). When all four system matrices commute, there exists a non-trivial set of coefficients \(\alpha_{i,j}\) such that
\begin{equation} 0 = \sum_{i=0}^k\sum_{j=0}^{m-k} \alpha_{i,j} A^iE^{m-i}B^{j}F^{m-j}, \end{equation}
for all values of \(0\leq k\leq m\).
Consider 4 commuting matrices of size \(m\times m\),\(A, E, B\) and \(F\), such that \((A,E)\) and \((B,F)\) form a regular matrix pencil. There exists a similarity transformation, represented by the square matrix \(U\) which is of full rank such that \((UEU^{-1},UAU^{-1},UFU^{-1},UBU^{-1})\) is placed in the canonical form. Define \(\bar{X} = UXU^{-1}\), where \(X\) is replaced by either \(E,A,F\) or \(B\). According to Theorem~\ref{thm:2S-CH} there exists a set of coefficients \(\alpha_{i,j}\) for which
\begin{equation} 0 = \sum_{i=0}^k\sum_{j=0}^{m-k} \alpha_{i,j} \bar{A}^i\bar{E}^{m-i}\bar{B}^{j}\bar{F}^{m-j}. \end{equation}
This can be rewritten as
\begin{equation} 0 = \sum_{i=0}^k\sum_{j=0}^{m-k} \alpha_{i,j} U{A}^i{E}^{m-i}{B}^{j}{F}^{m-j}U^{-1}. \end{equation}
Pre and post multiplying this expression respectively by \(U^{-1}\) and \(U\) gives
\begin{equation} 0 = \sum_{i=0}^k\sum_{j=0}^{m-k} \alpha_{i,j} {A}^i{E}^{m-i}{B}^{j}{F}^{m-j}, \end{equation}
which proof Theorem~\ref{thm:2S-ch2}.
Observability
Observability and the observability matrix have both been discussed in the previous chapter. To recap, we introduced two observability-like matrices, the observability matrix for multi-dimensional descriptor systems and the recursive observability matrix. For both matrices we also introduced their extended versions, which allow these two matrices to have an arbitrary number of rows\footnote{This is only true to some extend, as the number of rows of the extended observability matrix can only be some specific value, based on the block sizes. As for the recursive observability matrix, the number of rows is equal to the number of outputs times the two elements of the order. It is thus for example not possible to construct a recursive observability matrix for a two-dimensional system with a prime-number of rows.}. We briefly repeat the definitions of the aforementioned concepts and show the new structures and properties of the observability and recursive observability matrix.
A commuting descriptor system is observable if and only if the entire state sequence can be estimated based on a finite set of measurements and when the system matrices are known.
We have already shown that the state sequence of a descriptor system can be constructed based on the generalized state \(x\), as \(x[k,l] = C\mathcal{A}^k_{m-1}\mathcal{B}^{l}_{m-1}x\) for all \(0\leq k \leq m-1\) and \(0\leq l \leq m-1\). From this result we can derive the following lemma.
A commuting descriptor system is observable if and only if the generalized state vector can be estimated based on a finite set of output measurements and when the system matrices are known.
Assessing observability was previously done by calculating the rank of the observability matrix. We further showed that the rank of the observability and the recursive observability matrices where the same for two-dimensional commuting state space models, this will however not be the case for descriptor systems. Instead the recursive observability matrix has to be used.
The observability matrix
We define the observability matrix for two-dimensional commuting descriptor systems as follows;
The observability matrix for the two-dimensional commuting descriptor system of Equation~\eqref{eqn:DS2D} is defined as
\begin{equation} \obs = \begin{bmatrix} C\mathcal{A}_{m-1}^{0}\mathcal{B}_{m-1}^{0} \\ \hline C\mathcal{A}_{m-1}^{1}\mathcal{B}_{m-1}^{0} \\ C\mathcal{A}_{m-1}^{0}\mathcal{B}_{m-1}^{1} \\ \hline \vdots \\ \hline C\mathcal{A}_{m-1}^{m-1}\mathcal{B}_{m-1}^{0} \\ C\mathcal{A}_{m-1}^{m-2}\mathcal{B}_{m-1}^{1} \\ \vdots \\ C\mathcal{A}_{m-1}^{0}\mathcal{B}_{m-1}^{m-1}. \\ \end{bmatrix} \end{equation}
This matrix has the same structure as the observability matrix for commuting state space models.
The recursive observability matrix
We also define the recursive observability matrix for two-dimensional commuting descriptor systems as follows;
Consider the commuting descriptor system from Equation~\eqref{eqn:DS2D}. The recursive observability matrix is defined as
\begin{equation}\label{eqn:2DS-rec-obs} \robs = \begin{bmatrix} \robs_0 \\ \robs_1 \\ \vdots \\ \robs_{m-1} \end{bmatrix}, \end{equation}
where
\begin{equation} \robs_l = \begin{bmatrix} C \mathcal{A}_{m-1}^0 \mathcal{B}_{m-1}^l \\ C \mathcal{A}_{m-1}^1 \mathcal{B}_{m-1}^l \\ \vdots \\ C \mathcal{A}_{m-1}^{m-1} \mathcal{B}_{m-1}^l \\ \end{bmatrix}. \end{equation}
Observability criteria
Based on Lemma~\ref{lem:2DS-obs} we can formulate a condition to verify the observability of a commuting descriptor system. Consider the system from Equation~\eqref{eqn:DS2D} with output \(y[k,l]\in \real^q\) for \(0\leq k \leq m-1\) and \(0 \leq l \leq m-1\). Note that \(y[k,l] = C \mathcal{A}_{m-1}^k \mathcal{B}_{m-1}^l x\), using this relation we can write
\begin{equation} \mathcal{Y} = \begin{bmatrix} y[0,0] \\ y[1,0] \\ \vdots \\ y[m-1,0] \\ \hline y[0,1] \\ y[1,1] \\ \vdots \\ y[m-1,1] \\ \hline \vdots \\ \hline y[0,m-1] \\ y[1,m-1] \\ \vdots \\ y[m-1,m-1] \end{bmatrix} = \begin{bmatrix} C \mathcal{A}_{m-1}^0 \mathcal{B}_{m-1}^0 \\ C \mathcal{A}_{m-1}^1 \mathcal{B}_{m-1}^0 \\ \vdots\\ C \mathcal{A}_{m-1}^{m-1} \mathcal{B}_{m-1}^0 \\ \hline C \mathcal{A}_{m-1}^0 \mathcal{B}_{m-1}^1 \\ C \mathcal{A}_{m-1}^1 \mathcal{B}_{m-1}^1 \\ \vdots\\ C \mathcal{A}_{m-1}^{m-1} \mathcal{B}_{m-1}^1 \\ \hline \vdots\\ \hline C \mathcal{A}_{m-1}^0 \mathcal{B}_{m-1}^{m-1} \\ C \mathcal{A}_{m-1}^1 \mathcal{B}_{m-1}^{m-1} \\ \vdots\\ C \mathcal{A}_{m-1}^{m-1} \mathcal{B}_{m-1}^{m-1} \end{bmatrix} x = \robs x. \end{equation}
Note that we used all available data in the left hand side of the equality. The vector \(x\) can be estimated if and only if the matrix \(\robs\) is of full rank. This is summarized in the next theorem.
A commuting descriptor system is observable if and only if the associated recursive observability matrix is of full rank.
We now face a problem; \textit{this theorem is not valid for the observability matrix!} We can demonstrate this easily with a counter example;
- Pick a system which is observable, according to Definition~\ref{def:2DS-obs}.
- Construct the observability matrix and verify the rank.
Such an example is the topic of the next section.
Example
Consider the commuting descriptor system with system matrices
\begin{equation} A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, E = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, F = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \end{equation}
and output matrix
\begin{equation} C = \begin{bmatrix} 1 & 1 \end{bmatrix}. \end{equation}
To verify the observability of this system we use Theorem~\ref{thm:2Ds-obs} and construct the recursive observability matrix
\begin{equation} \robs = \begin{bmatrix} C \mathcal{A}_{1}^0 \mathcal{B}_{1}^{0} \\ C \mathcal{A}_{1}^1 \mathcal{B}_{1}^{0} \\ \hline C \mathcal{A}_{1}^0 \mathcal{B}_{1}^{1} \\ C \mathcal{A}_{1}^1 \mathcal{B}_{1}^{1} \end{bmatrix} = \begin{bmatrix} C EF \\ C AF \\ \hline C EB \\ C AB \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ \hline 1 & 0 \\ 1 & 1 \end{bmatrix} \end{equation}
This matrix has rank 2 which proofs that the system is observable. We can also construct the observability matrix. This matrix is
\begin{equation} \begin{bmatrix} C \mathcal{A}_{1}^0 \mathcal{B}_{1}^{0} \\ \hline C \mathcal{A}_{1}^1 \mathcal{B}_{1}^{0} \\ C \mathcal{A}_{1}^0 \mathcal{B}_{1}^{1} \end{bmatrix} = \begin{bmatrix} C EF \\ \hline C AF \\ C EB \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ \hline 1 & 0 \\ 1 & 0 \end{bmatrix} \end{equation}
The rank of this matrix is 1. This counter example demonstrates that the rank of the observability matrix can not be used to asses the controllability property of commuting descriptor systems.
The singular-singular part is missing
To understand why the observability matrix is not suitable to determine the observability of a commuting described systems we can look at the Figure \ref{fig:2S-1}, which shows the data dependency of the regular and singular parts of the state vector. Multiplying the observability matrix from the previous example with the generalized state vector gives
\begin{equation}\label{eqn:2S-example} \begin{bmatrix} C EF \\ \hline C AF \\ C EB \end{bmatrix}x = \begin{bmatrix} y[0,0] \\ \hline y[1,0] \\ y[0,1] \end{bmatrix}. \end{equation}
The data point \(y[1,1]\), which is the only point affect by the $SS$-part of the state vector, is not included in Equation \eqref{eqn:2S-example}.
Controllability
Dual to observability, we can introduce the concept of controllability and the thereby associated (recursive) state sequence matrices.
The state sequence matrix
We define the state sequence matrix for two-dimensional commuting descriptor systems as follows;
The state sequence matrix for the two-dimensional commuting descriptor system of Equation~\eqref{eqn:DS2D} is defined as
\begin{equation} X = \begin{bmatrix} X_0 & X_2 & \cdots & X_{m-1} \end{bmatrix} \end{equation}
with
\begin{equation} X_i = \begin{bmatrix} \mathcal{A}_{m-1}^{i}\mathcal{B}_{m-1}^{0}x & \mathcal{A}_{m-1}^{i-1}\mathcal{B}_{m-1}^{1}x & \cdots & \mathcal{A}_{m-1}^{0}\mathcal{B}_{m-1}^{i}x \end{bmatrix} \end{equation}
This matrix has the same structure as the state sequence matrix for commuting state space models.
The recursive state sequence matrix
We also define the recursive state sequence matrix for commuting descriptor systems as follows;
Consider the commuting descriptor system from Equation~\eqref{eqn:DS2D} with generalized state vector \(x\). The recursive state sequence matrix is defined as
\begin{equation}\label{eqn:2DS-rec-cont} \rX = \begin{bmatrix} \rX_0 & \rX_1 & \cdots & \rX_{m-1} \end{bmatrix}, \end{equation}
where
\begin{equation} \rX_l = \begin{bmatrix} \mathcal{A}_{m-1}^0 \mathcal{B}_{m-1}^lx & \mathcal{A}_{m-1}^1 \mathcal{B}_{m-1}^lx & \cdots & \mathcal{A}_{m-1}^{m-1} \mathcal{B}_{m-1}^lx & \end{bmatrix}. \end{equation}
A commuting descriptor system is controllable if and only if the recursive state sequence matrix has full rank. This proof follows the same reasoning as for the case of observability.
Observability and controllability in the WCF
In the previous 2 sections, we derived two expressions for the recursive observability and the recursive state sequence matrices for descriptor systems parameterized by 4 commuting system matrices. In this section we will look at the structure of these matrices when the descriptor system is placed in the WCF.
The extended recursive observability matrix of order \((\mu,\nu)\), denoted by \(\robs_{0|\mu-1,0|\nu-1}\), for the descriptor system presented in Equation~\eqref{eqn:WCF2d} is
\begin{equation}\label{eqn:2DS-obs-wcf-full} \resizebox{.88\hsize}{!}{\( \begin{bmatrix} C_{RR} & {C_{SR}E_{{1}}^{\mu-1}} & {C_{RS}F_{{1}}^{\nu-1}} & {C_{SS}E_{{2}}^{\mu-1}F_{{2}}^{\nu-1}} \\ C_{RR}A_{{1}} & C_{SR}E_{{1}}^{\mu-2} & C_{RS}A_{{2}}F_{{1}}^{\nu-1} & C_{SS}E_{{2}}^{\mu-2}F_{{2}}^{\nu-1} \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}} & {C_{SR}} & {C_{RS}A_{{2}}^{\mu-1}F_{{1}}^{\nu-1}} & {C_{SS}F_{{2}}^{\nu-1}} \\ \hline C_{RR}B_{1} & {C_{SR}E_{{1}}^{\mu-1}}B_{2} & {C_{RS}F_{{1}}^{\nu-2}} & {C_{SS}E_{{2}}^{\mu-1}F_{{2}}^{\nu-2}} \\ C_{RR}A_{{1}}B_{1} & C_{SR}E_{{1}}^{\mu-2}B_{2} & C_{RS}A_{{2}}F_{{1}}^{\nu-2} & C_{SS}E_{{2}}^{\mu-2}F_{{2}}^{\nu-2} \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}}B_{1} & {C_{SR}}B_{2} & {C_{RS}A_{{2}}^{\mu-1}F_{{1}}^{\nu-2}} & {C_{SS}F_{{2}}^{\nu-2}} \\ \hline \vdots & \vdots & \vdots & \vdots \\ \hline C_{RR}B_{1}^{\nu-1} & {C_{SR}E_{{1}}^{\mu-1}}B_{2}^{\nu-1} & C_{RS} & {C_{SS}E_{{2}}^{\mu-1}} \\ C_{RR}A_{{1}}B_{1}^{\nu-1} & C_{SR}E_{{1}}^{\mu-2}B_{2}^{\nu-1} & C_{RS}A_{{2}} & C_{SS}E_{{2}}^{\mu-2} \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}}B_{1}^{\nu-1} & {C_{SR}}B_{2}^{\nu-1} & {C_{RS}A_{{2}}^{\mu-1}} & C_{SS} \end{bmatrix} \)} \end{equation}
This matrix is the collection of 4 recursive observability matrix, we can write
\begin{equation} \robs_{0|\mu-1,0|\nu-1} = \begin{bmatrix} \robs_{RR} & \robs_{SR} & \robs_{RS} & \robs_{SS} \end{bmatrix}, \end{equation}
where the subscripts indicate
- \(RR\): regular-regular part,
- \(SR\): singular-regular part,
- \(RS\): regular-singular part,
- \(SS\): singular-singular part.
We dropped the order indication to keep the notation as concise as possible. These 4 extended recursive observability matrices are associated to the 4 subsystems depicted in Table~\ref{tbl:overview-of-partial-moddels}. Due to the nilpotency of the 4 matrices \(E_1,E_2,F_1\) and \(F_2\) we can rewrite Equation~\eqref{eqn:2DS-obs-wcf-full} as
\begin{equation}\label{eqn:2DS-obs-wcf-sparse} \robs_{0|\mu-1,0|\nu-1} = \begin{bmatrix} C_{RR} & 0 & 0 & 0 \\ C_{RR}A_{{1}} & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}} & C_{SR} & 0 & 0 \\ \hline C_{RR}B_{1} & 0 & 0 & 0 \\ C_{RR}A_{{1}}B_{1} & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}}B_{1} & {C_{SR}}B_{2} & 0 & 0 \\ \hline \vdots & \vdots & \vdots & \vdots \\ \hline C_{RR}B_{1}^{\nu-1} & 0 & C_{RS} & 0 \\ C_{RR}A_{{1}}B_{1}^{\nu-1} & 0 & C_{RS}A_{2} & 0 \\ \vdots & \vdots & \vdots & \vdots \\ {C_{RR}A_{{1}}^{\mu-1}}B_{1}^{\nu-1} & {C_{SR}}B_{2}^{\nu-1} & C_{RS}A_{{2}}^{\mu-1} & C_{SS} \end{bmatrix} \end{equation}
This structure will be important when discussing the gap for multi-dimensional descriptor systems in the next section.
Mind the gap
The so called gap has been introduced in the case of one-dimensional descriptor systems in Chapter~\ref{ch:1DS}. Recall that the gap was a collection of rows of the observability matrix which are linearly dependent on the first \(m_r\) rows of the observability matrix, where \(m_r\) is equal to the number of causal solutions. After the gap, the rows of the observability became linearly independent due to the non-causal solutions of the descriptor system.
In this section we discuss this gap phenomena for the recursive observability matrix. The observability matrix for two-dimensional descriptor systems is not discussed as it is not compatible with descriptor systems.
Two interpretation, three gaps
Before we start the general discussion, we introduce a small example. The example systems is a two-dimensional commuting descriptor system of order 4. Order 4 is the smallest order such that all 4 types of solutions; \(RR\), \(RS\), \(SR\), and \(SS\) are included in the output. The descriptor system is given by
\begin{equation} \begin{aligned} E x[k+1,l] = & A x[k,l] \\ F x[k,l+1] = & B x[k,l] \\ y[k,l] = & C x[k,l], \end{aligned} \end{equation}
with four system matrices
\begin{equation} A = \begin{bmatrix} 1 & & & \\ & 1 & & \\ & & 1 & \\ & & & 1 \\ \end{bmatrix}, E = \begin{bmatrix} 1 & & & \\ & 0 & & \\ & & 1 & \\ & & & 0 \\ \end{bmatrix}, \end{equation}
\begin{equation} B = \begin{bmatrix} 1 & & & \\ & 1 & & \\ & & 1 & \\ & & & 1 \\ \end{bmatrix}, F = \begin{bmatrix} 1 & & & \\ & 1 & & \\ & & 0 & \\ & & & 0 \\ \end{bmatrix}, \end{equation}
and output matrix
\begin{equation} C = \begin{bmatrix} 1 &1 &1 &1 \end{bmatrix}. \end{equation}
This system is placed in the Weierstrass canonical form and we can directly calculate the recursive observability matrix, which has order \((4,4)\), i.e.~the matrix consists of 4 blocks which each has 4 rows
\begin{equation}\label{2S-obs-example} \robs = \begin{bmatrix} \mathbf{C\mathcal{A}_{3}^{0}\mathcal{B}_{3}^{0}} \\ C\mathcal{A}_{3}^{1}\mathcal{B}_{3}^{0} \\ C\mathcal{A}_{3}^{2}\mathcal{B}_{3}^{0} \\ C\mathcal{A}_{3}^{3}\mathcal{B}_{3}^{0} \\ \hline \mathbf{C\mathcal{A}_{3}^{0}\mathcal{B}_{3}^{1}} \\ C\mathcal{A}_{3}^{1}\mathcal{B}_{3}^{1} \\ C\mathcal{A}_{3}^{2}\mathcal{B}_{3}^{1} \\ C\mathcal{A}_{3}^{3}\mathcal{B}_{3}^{1} \\ \hline C\mathcal{A}_{3}^{0}\mathcal{B}_{3}^{2} \\ C\mathcal{A}_{3}^{1}\mathcal{B}_{3}^{2} \\ C\mathcal{A}_{3}^{2}\mathcal{B}_{3}^{2} \\ C\mathcal{A}_{3}^{3}\mathcal{B}_{3}^{2} \\ \hline \mathbf{C\mathcal{A}_{3}^{0}\mathcal{B}_{3}^{3}} \\ C\mathcal{A}_{3}^{1}\mathcal{B}_{3}^{3} \\ C\mathcal{A}_{3}^{2}\mathcal{B}_{3}^{3} \\ \mathbf{C\mathcal{A}_{3}^{3}\mathcal{B}_{3}^{3}} \end{bmatrix} = \begin{bmatrix} \mathbf{1} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \mathbf{1} & \mathbf{1} & \mathbf{0} & \mathbf{0} \\ \hline 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ \hline 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ \hline \mathbf{1} & \mathbf{0} & \mathbf{1} & \mathbf{0} \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} \\ \end{bmatrix}. \end{equation}
The presented system is observable as the recursive observability \(\robs\) has rank \(4\). The bold rows in this matrix are the first four linearly independent rows that occur in this matrix, counting from the top row down. The linearly independent rows are structured in a particular way, to understand this structure, we look at two interpretations of the recursive observability matrix;
- the recursive observability matrix as a block (one-dimensional) observability matrix,
- the recursive observability matrix as a collection of (one-dimensional) observability matrices.
In the first interpretation the observability matrix from Equation~\eqref{2S-obs-example} is equivalent to the observability matrix of the one-dimensional descriptor system
\begin{equation} \begin{aligned} F x[l+1] = B x[l] \\ y[l] = \begin{bmatrix} C \mathcal{A}_{3}^0 \\ C \mathcal{A}_{3}^1 \\ C \mathcal{A}_{3}^2 \\ C \mathcal{A}_{3}^3 \\ \end{bmatrix} x [l] = C_1 x[l] \end{aligned} \end{equation}
In this case, the output matrix \(C_1\) is explicitly equal to
\begin{equation} C_1 = \begin{bmatrix} C \mathcal{A}_{3}^0 \\ C \mathcal{A}_{3}^1 \\ C \mathcal{A}_{3}^2 \\ C \mathcal{A}_{3}^3 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 \\ \end{bmatrix} \end{equation}
The observability matrix of this system is exactly equal to the matrix in Equation~\eqref{2S-obs-example}. As this system is now a one-dimension descriptor system, we can use the techniques establish before, to determine the gap in the observability matrix. The system matrix \(F\) has a single eigenvalue \(0\) with algebraic multiplicity \(1\), from which is follows that the last block row is linearly independent. This is true, as shown in Equation~\eqref{2S-obs-example}.
The second interpretation looks at the recursive observability as a collection of individual observability matrices, multiplied from the right by a matrix \(\mathcal{B}_{3}^l\), for some \(0\leq l \leq 3\). The observability matrix is
\begin{equation} \begin{bmatrix} C\mathcal{A}_{3}^{0} \\ C\mathcal{A}_{3}^{1} \\ C\mathcal{A}_{3}^{2} \\ C\mathcal{A}_{3}^{3} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{1} & \mathbf{0} & \mathbf{1} & \mathbf{0} \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} \\ \end{bmatrix}. \end{equation}
The first and last row is linearly independent. Note, that this system by itself is not observable.
From both interpretation of the recursive observability matrix we can draw two conclusions;
- the last block(s) of the recursive observability matrix can be linearly independent,
- the last row(s) in each block can be linearly independent.
In total we can identify three gaps in the recursive observability matrix;
- a gap between the \textbf{last} rows of the \textbf{first} blocks,
- a gap between the \textbf{first} rows of the \textbf{last} blocks,
- a gap between the \textbf{last} rows of the \textbf{last} blocks.
These three gaps separate the three different solutions that we identified in the canonical form for two-dimensional commuting descriptor systems being \(RR\), \(RS\), \(SR\) and \(SS\). The gap structure for this example is shown in Figure~\ref{fig:2s-gap-example} where the recursive observability matrix is depicted for different orders, ranging from \((4,4)\) to \((6,6)\).
Slicing the recursive observability matrix
Before we continue the general derivation for the expression of the gap, we will first introduce a method to select a certain subset of rows of the recursive observability matrix.
The number rows of an extended recursive observability matrix is determined by two factors; the size of the output matrix \(C\) and the order of the system. For a system with \(q\) outputs, and a order \((\mu,\nu)\) we have shown that the number of rows of the extended recursive observability matrix \(\Gamma_{0|\mu-1,0|\nu-1}\) is \(q\mu\nu\), i.e.~the matrix consist of \(\mu\) blocks, where every block has \(\nu\) block-rows and every block row has \(q\) rows.
We now define the selector operator \(S_{i_1|n_1,i_2|n_2}^{\mu,\nu}\), which selects specific rows of \(\Gamma_{0|\mu-1,0|\nu-1}\) as
\begin{equation} S_{i_1|n_1,i_2|n_2}^{\mu,\nu} \Gamma_{0|\mu-1,0|\nu-1} = \Gamma_{i_1|n_1,i_2|n_2}^{\mu,\nu}. \end{equation}
The matrix \(\Gamma_{i_1|n_1,i_2|n_2}^{\mu,\nu}\) is than equal to
\begin{equation} \Gamma_{i_1|n_1,i_2|n_2}^{\mu,\nu} = \begin{bmatrix} C\mathcal{A}^{i_1}_{\mu-1}\mathcal{B}^{i_2}_{\nu-1} \\ C\mathcal{A}^{i_1+1}_{\mu-1}\mathcal{B}^{i_2}_{\nu-1} \\ \vdots \\ C\mathcal{A}^{n_1}_{\mu-1}\mathcal{B}^{i_2}_{\nu-1} \\ \hline C\mathcal{A}^{i_1}_{\mu-1}\mathcal{B}^{i_2+1}_{\nu-1} \\ C\mathcal{A}^{i_1+1}_{\mu-1}\mathcal{B}^{i_2+1}_{\nu-1} \\ \vdots \\ C\mathcal{A}^{n_1}_{\mu-1}\mathcal{B}^{i_2+1}_{\nu-1} \\ \hline \vdots \\ \hline C\mathcal{A}^{i_1}_{\mu-1}\mathcal{B}^{n_2}_{\nu-1} \\ C\mathcal{A}^{i_1+1}_{\mu-1}\mathcal{B}^{n_2}_{\nu-1} \\ \vdots \\ C\mathcal{A}^{n_1}_{\mu-1}\mathcal{B}^{n_2}_{\nu-1} \\ \end{bmatrix} \end{equation}
The selector operator \(S_{i_1|n_1,i_2|n_2}^{\mu,\nu}\) therefor selects the blocks ranging from block-index \(i_2\) until \(n_2\), both ends included, and from every one of these blocks it selects rows ranging from the row index \(i_1\) until \(n_1\), again both ends included. The new matrix \(\Gamma_{i_1|n_1,i_2|n_2}^{\mu,\nu}\) has a total of \(q(n_1-i_1+1)(n_2-i_2+1)\) rows. In order for the selection to be well defined we have to restrict the index range of the selector matrix, such that the selected ranges do not exceed the row ranges of the extended recursive observability matrix. We have that \(0\leq i_1 \leq n_i \leq \mu-1\) and \(0\leq i_1 \leq n_1 \leq \nu-1\).
Selecting rows of a matrix is a linear operations and can be represented as a matrix multiplication. The selection matrix is equal to
\begin{equation} S_{i_1|n_1,i_2|n_2}^{\mu,\nu} = S_{i_2|n_2}^{\nu} \kron S_{i_1|n_1}^{\mu}, \end{equation}
where \(S_{i|n}^{\mu}\) is the matrix obtained by selecting the rows ranging from \(i\) until \(n\) from the identity matrix of size \(\mu \times \mu\). Note that the order of the Kronecker multiplication is different that the order in the subscript. As an example consider the matrix \(S_{1|2,0|1}^{3,3}\), this matrix is equal to
\begin{equation} S_{1|2,0|1}^{3,3} = S_{0|1}^3 \kron S_{1|2}^3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \kron \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix} \end{equation}
Multiplying this matrix with the recursive observability of the third order descriptor systems gives
\begin{equation} S_{1|2,0|1}^{3,3}\Gamma_{0|2,0|2} = \Gamma_{1|2,0|1}^{3,3} = \begin{bmatrix} C\mathcal{A}_2^{1}C\mathcal{B}_2^{0} \\ C\mathcal{A}_2^{2}C\mathcal{B}_2^{0} \\ \hline C\mathcal{A}_2^{1}C\mathcal{B}_2^{1} \\ C\mathcal{A}_2^{2}C\mathcal{B}_2^{1} \end{bmatrix} \end{equation}
Analyzing the gap in the WCF
In the previous section we developed some intuition about the gap for a two-dimensional systems. We will now look at the details for when the system is placed in the WCF. The operation of placing the system in the WCF, does not change the linearly independent rows of the observability matrix, it only affects the sparsity structure.
In section \ref{sec:2DS-obs-wcf}, we have shown that the recursive observability matrix of a two-dimensional descriptor systems consists of four parts indicated as \(\robs_{RR}, \robs_{SR}, \robs_{RS}\) and \(\robs_{SS}\), each part is the \gls{EROM} of the associated descriptor system, presented in Table \ref{tbl:overview-of-partial-moddels}. Denote the order of each subsystem by \(m_{RR}, m_{RS}, m_{SR}\) and \(m_{SS}\) and the order of the extended observability matrix as \((\mu,\nu)\). We assume that both \(\mu\) and \(\nu\) are sufficiently large, i.e.~a lot larger that the order of the system. In the following discussion, this notion will be made clear.
Next we are going to slice the \gls{EROM} and discuss the rank of all relevant matrix slices. The rank of all slices can that be composed into a rank atlas as show for example in Figure \ref{fig:2DS-rank-atlas}, which is an image of the rank as a function of the size of the slices.
To start, take the sliced matrix \(S_{0|m_r,0|m_r}^{\mu,\nu}\Gamma_{RR}\). This matrix coincides with the recursive observability matrix of the $RR$-subsystem. If the system is observable, this matrix has full rank and we have that
\begin{equation} \rank{S_{0|m_r,0|m_r}^{\mu,\nu}\Gamma_{RR}} = \rank{S_{0|m_r+1,0|m_r+1}^{\mu,\nu}\Gamma_{RR}} = m_{RR}. \end{equation}
When the order \((\mu,\nu)\) is large enough we also have
\begin{equation} S_{0|m_r,0|m_r}^{\mu,\nu}\Gamma_{SR} = S_{0|m_r,0|m_r}^{\mu,\nu}\Gamma_{RS} = S_{0|m_r,0|m_r}^{\mu,\nu}\Gamma_{SS} = 0. \end{equation}
This is true under the condition than;
- The value \(m_{RS}\) is smaller that \(\mu-m_r\), which implies that ever block of \(\Gamma_{RS}\) has at most \(m_{SR}\) non-zero trailing rows, which are not included in the slice \(S_{0|m_r,0|m_r}^{\mu,\nu}\).
- The value \(m_{SR}\) is smaller that \(\nu-m_r\), which implies that \(\Gamma_{SR}\) has at most \(m_{SR}\) non-zero trailing blocks, which are not included in the slice \(S_{0|m_r,0|m_r}^{\mu,\nu}\).
- The value \(m_{SS}\) is smaller that \(\mu-m_r\) or \(\nu-m_r\) , which implies that \(\Gamma_{SS}\) has at most \(m_{SS}\) non-zero trailing blocks, with each of these blocks having at most \(m_{SS}\) trailing non-zero rows, which are not included in the slice \(S_{0|m_r,0|m_r}^{\mu,\nu}\).
Note that we used the fact that the nilpotency index of a matrix is bound from above by the number of rows/columns of the matrix.
If we now start to include more and more rows in the matrix slices, all of the sudden, the first condition in the list above will not be true anymore, and the non-zero rows of \(\Gamma_{SR}\) will start to add to the rank of the sliced \gls{EROM} and at some point when we have included \(k\) rows we have
\begin{equation} \rank{S_{0|m_r,0|k}^{\mu,\nu}\Gamma_{SR} } \neq \rank{S_{0|m_r,0|k+1}^{\mu,\nu}\Gamma_{SR} } \end{equation}
This is the first gap. Next, instead of increasing the number of rows in our slices, we increase the number of blocks. At some point the non-zero trailing blocks of \(\Gamma_{RS}\) will start to affect the rank and
\begin{equation} \rank{S_{0|l,0|m_r}^{\mu,\nu}\Gamma_{RS} } \neq \rank{S_{0|l+1,0|m_r}^{\mu,\nu}\Gamma_{SR}} \end{equation}
for some number of blocks, indicated with \(l\). This is also part of the first gap.
To understand the second gap and the third gap, we have to look at the dynamic relations between the last blocks and last rows of all blocks of respectively \(\Gamma_{RS}\) and \(\Gamma_{SR}\). Both matrices have a regular component, and according to the theorem of Cayley–Hamilton, only the first \(m_{RS}\) blocks will be linearly independent and only the first \(m_{SR}\) last rows of each block will be linearly independent. Resulting in the stabilization of the gap, both stabilizations form the second and third gap.
Finally when increasing the order even further, we start to include the last rows of the last blocks. These rows are non-zero in the matrix \(\Gamma_{SS}\) and start to contribute to the rank.
From this analysis we can define a rank atlas of the extended recursive observability matrix. The rank atlas is a two-dimensional discrete indexed function which maps the rank of each slice to the number of rows and blocks of these slices. An example of the rank atlas for a state space model of at least order 16 has been shown in Figure \ref{fig:2DS-rank-atlas}. On the right side of the figure, we have shown the full structure of the \gls{EROM} of order \((10,10)\).
Given an extended recursive observability matrix \(\Gamma_{0|\mu-1,0|\nu-1}\) of order \((\mu,\nu)\). The rank atlas is a function
\begin{equation} f[k,l] = \rank{S_{0|k,0|l}^{\mu,\nu}\Gamma_{0|\mu-1,0|\nu-1}} \end{equation}
If you reached this far in the analysis, you probably ask yourself the question; \textit{how can this be generalized to higher-dimensions?} The answer is simple and, the selection matrices are extended to include thee indices, rows, blocks and sets of blocks. Now we make the distinction between 8 subsystem\footnote{In every dimension we can have a causal and non-causal part and all combination can occur. This gives a total of \(2^{3}\) possibilities.}: \(RRR\), \(SRR\), \(RSR\), \(SSR\), \(RRS\), \(SRS\), \(RSS\), \(SSS\). The rank atlas for this case, together with the explicit sparsity structure of the \gls{EROM} is shown in Figure \ref{fig:2DS-rank-atlas-3d}.
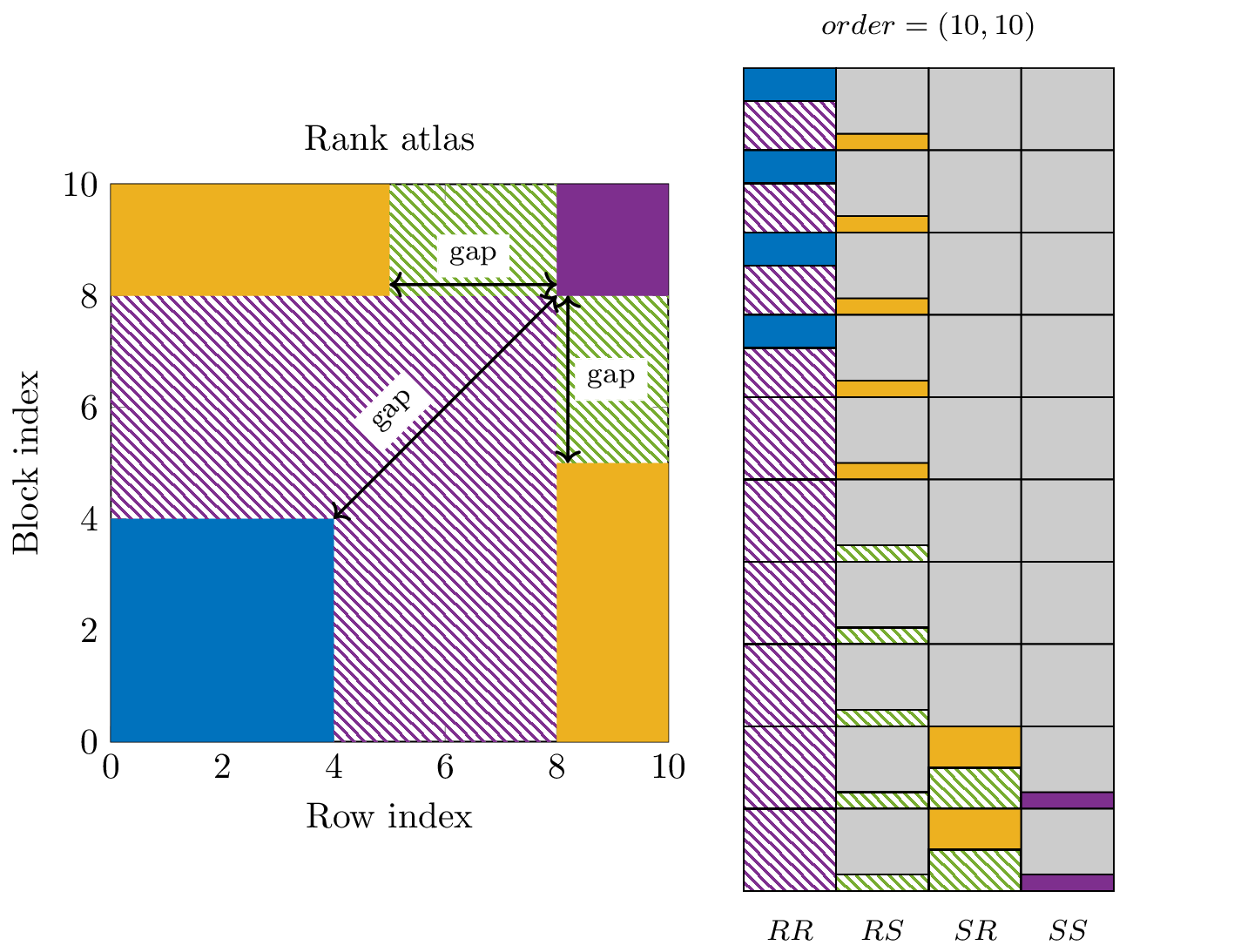
Figure 3: In this figure the rank atlas, together with the corresponding rows of the gls{EROM} are shown. The colors in the left and right plot coincide with each other. In total, we can identify three gaps.
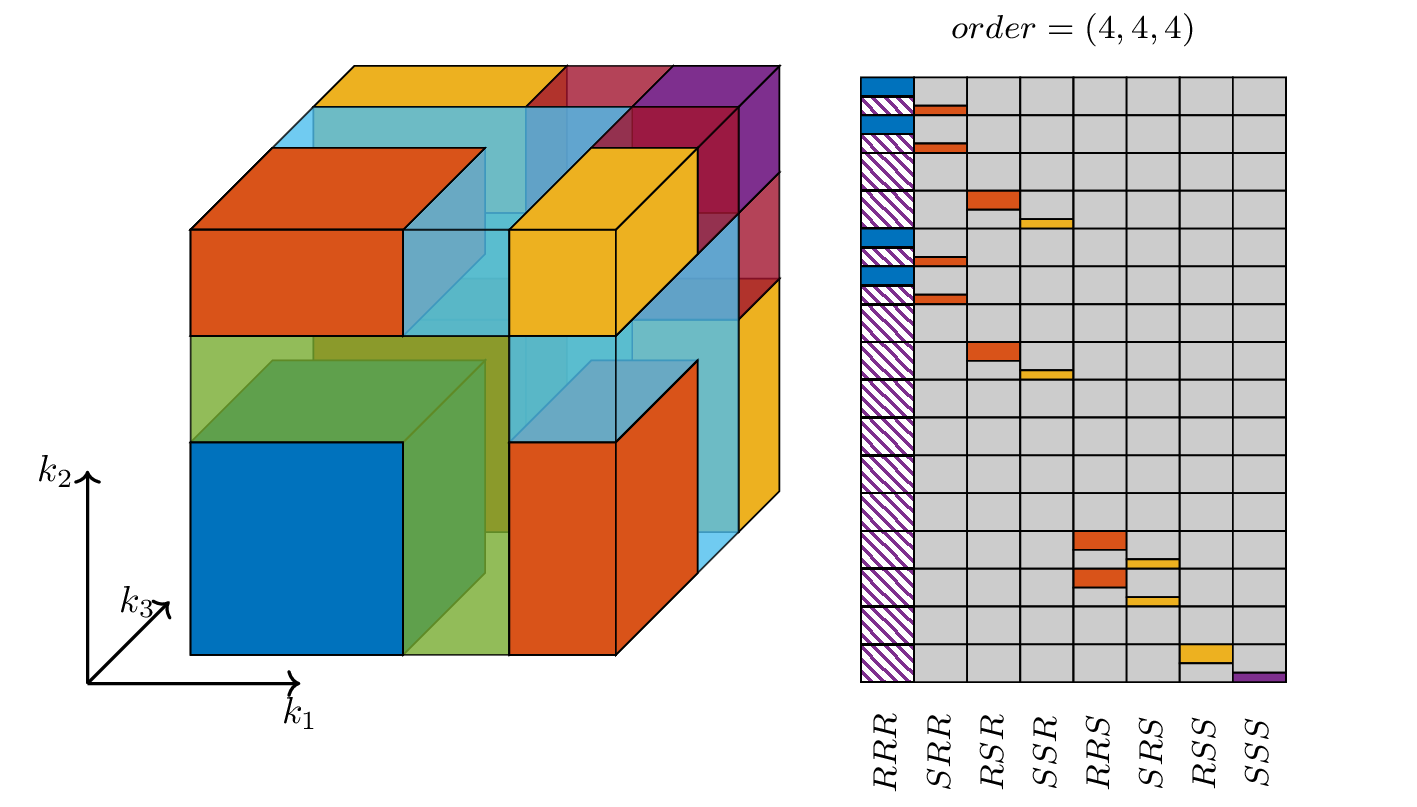
#+caption[Rank atlas of an extended recursive observability matrix for a three-dimensional commuting descriptor system.]: This is the rank atlas for a three-dimensional commuting state space model. In total 8 different types of solutions can be identified. The colors in the left and right plot coincide with each other.
Conclusion
The necessary conditions for the existence of a non-trivial state sequence \(x[k,l]\) of a two-dimensional descriptor system has been derived. The derivation is based on the classical results of the Weierstrass canonical form. We have proven that a descriptor system is well-posed if and only if it can be be transformed to the multidimensional generalization of the Weierstrass canonical form.
This results allowed us to define four kind of solutions, classified by the causal/non-causal behaviors of the state sequence. These four solution can also be found in the structure of the recursive observability matrix, and explain the multiple gaps in the row space of this matrix.
A good understanding of the different types of solutions for the commuting descriptor system is important to derive a realization algorithm for this class of systems in the next chapters.